The editing operations in this section break objects apart, cut holes in them, and put them back together. Some of these commands connect curves to curves or surfaces to surfaces or polysurfaces and break a composite curve or polysurface into its components.
The commands: Join, Explode, Trim, and Split apply to curves, surfaces, and polysurfaces.
The Rebuild, ChangeDegree, and Smooth commands alter the shape of a curve or surface by changing its underlying control point structure.
In addition, objects have properties that are assigned to them such as color, layer, rendering material, and other attributes depending on the object. The Properties command manages these properties.
The Join command connects curves or surfaces together into one object. For example, a polycurve can consist of straight-line segments, arcs, polylines, and free-form curves. The Join command also connects adjacent surfaces into a polysurface.
The Explode command removes the connection between joined curves or surfaces. For polysurfaces, this is useful if you want to edit each individual surface with control points.
The Trim and Split commands are similar. The difference is when you trim an object, you select the parts to remove and they are deleted. When you split an object, all parts are left.
The Split command will split a surface with a curve, surface, polysurface, or its own isoparametric curves.
The Untrim command removes a surface’s trimming curve, with an option to keep the curve so you can re-use it.
You can make subtle changes in the shape of a curve or surface by moving the location of its control points. Rhino offers many tools for editing control points. Some commands such as Rebuild, Fair, and Smooth offer some automated solutions for redistributing control points over a curve or surface. Other commands, such as control point dragging and nudging,
To edit curves and surfaces by manipulating control points, use the PointsOn command to turn the control points on.
When you are finished with control-point editing, use the PointsOff command or press Esc to turn them off.
Control points of polysurfaces cannot be turned on for editing. Editing the control points of polysurfaces could separate the edges of the joined surfaces creating “leaks” in the polysurface.
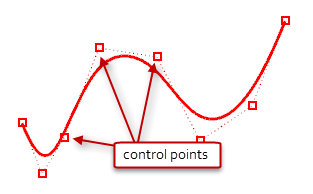
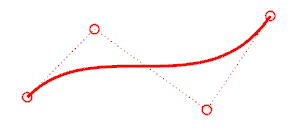
When you move control points, the curve or surface changes, and Rhino smoothly redraws it. The curve or surface is not drawn though the control points rather it is attracted to the new positions of the control point. This allows the object to be smoothly deformed. When control points are on, Rhino’s transform commands can manipulate the points. You can also rebuild surfaces to add control points and redistribute them.
Adding control points to a curve gives you more control over the shape of the curve. Manipulating control points also lets you remove kinks, make curves uniform, and add or subtract detail. The Delete key erases curve control points. This changes the shape of the curve.
A polynomial is a function like y = 3x3 –2x +1. The "degree" of the polynomial is the largest power of the variable. For example, the degree of 3x3 –2x + 1 is 3; the degree of –x5 + x2 is 5, and so on. NURBS functions are rational polynomials and the degree of the NURBS is the degree of the polynomial. From a NURBS modeling point of view, the (degree –1) is the maximum number of "bends" you can get in each span.
For example:
A degree-1 curve must have at least two control points.
A line has degree less than 1. It has zero bends.

A degree-2 curve must have at least three control points.
A parabola, hyperbola, arc, and circle (conic section curves) have degree less than 2. They have one bend.
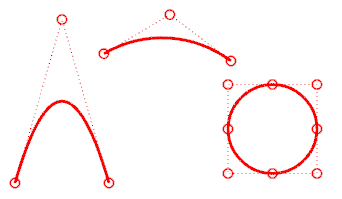
A degree-3 curve must have at least four control points.
A cubic Bézier has degree less than 3 If you arrange its control points in a zig-zag shape, you can get two bends.