The ChangeDegree command changes the degree of the polynomial that defines the curve or surface by adding or subtracting control points between knot spans, while maintaining the knot structure.
Steps
| 1. | Select the objects. |
| 2. | Type a degree value. For surfaces type values in the u- and v-directions. |
Command-line option
Deformable=Yes / No
If Yes, and the degree of the curve/surface is different from the requested degree, the new curve/surface has simple interior knots.
If No, and the degree of the curve/surface is LESS than the requested degree, the new curve/surface will have exactly the same geometry and parameterization as the original, but it will have knots of multiplicity = old multiplicity + new degree - old degree.
If the degree of the curve/surface is GREATER than the requested degree, then the new curve/surface will be an approximation of the original with simple knots.
Note
| ● | The ChangeDegree command changes the degree of the polynomial Rhino uses to create the curve. It keeps the knot structure of the curves the same, but it adds or subtracts control points between each knot span. |
| ● | Often it is better to use InsertKnot and RemoveKnot instead of ChangeDegree, because you can add/remove control points more locally. |
| ● | If you want the surface to have the same geometry, but more control points for editing, then try increasing the degree to 5 with the Deformable option set to No. In this case, you may want to consider using the InsertKnot command, which will add control points but leave the degree unchanged. |
| ● | If you are going to export your geometry to another application, make every attempt to keep the degree of your surfaces low. In particular, many mechanical CAD systems cannot import surfaces that have degrees greater than 3. |
| ● | The number of control points you add or subtract depends on the degree; the higher the degree, the greater the number of control points. |
| ● | If you raise the degree of a surface with Deformable=No, it will no longer be periodic. Use MakePeriodic to restore the periodicity of the surface. |
| ● | Objects with higher degrees take longer to display and use more memory. |
A polynomial is a function like (y= 3x3-2x+1). The degree of the polynomial is the largest power of the variable. For example, the degree of (3x3-2x+2) is 3; the degree of (-x5+x2) is 5, and so on. NURBS functions are rational polynomials and the degree of the NURBS is the degree of the polynomial. From a NURBS modeling point of view, the (degree –1) is the maximum number of "bends" you can get in each span.
For example:
A line has degree 1. It has zero "bends."

Degree 1: line.
A parabola, hyperbola, arc, and circle (conic section curves) have degree 2. They have one bend.
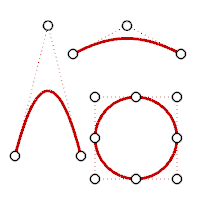
Degree 2: parabola, arc, circle.
A cubic Bézier has degree 3. If you arrange its control points in a zigzag shape, you can get two bends.
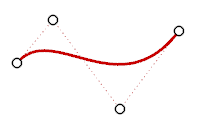
Degree 3 curve.
See also
Rhinoceros 5 © 2010-2015 Robert McNeel & Associates. 17-Sep-2015