
六个矩形的曲面或网格可以形成一个包围封闭空间的立方体。
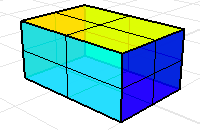
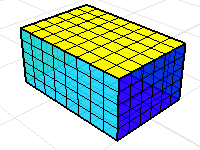
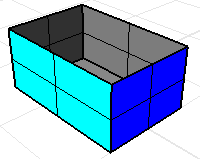
只要这个立方体少了一个面,体积质量属性指令计算出来的是没有意义的结果。

计算体积质量属性的指令选取的物件必需可以包围一个封闭空间,要符合这个要求最简单的方法是选取实体物件 (封闭、流形而且曲面的法线方向全部朝外) 做计算,但有些情形将物件组合成实体会造成某些不便。
遇到这种情形时,您可以选取一组非实体的物件来计算体积质量属性。
您必需确认:
| ● | 所有的物件可以包围一个封闭的空间。 |
| ● | 每一个物件必需是封闭空间的外壁,不可以位于内部。 |
| ● | 所有曲面或网格的法线方向必需朝外。 |
步骤
| 4 | 使用 Dir 指令检查或反转曲面或网格的法线方向。
六个矩形的曲面或网格可以形成一个包围封闭空间的立方体。
只要这个立方体少了一个面,体积质量属性指令计算出来的是没有意义的结果。
|
多重曲面或网格的每一个边缘都被两个面共用称为流形,体积质量属性指令会认为这些面包围着一个封闭空间。
所有曲面未能包围封闭空间的非流形多重曲面计算出来的体积质量属性并没有意义。
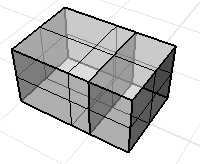
所有曲面可以包围封闭空间的非流形多重曲面可以正确计算体积质量属性。
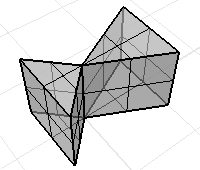
多重曲面或网格可能有法线方向不一致的情形。
使用 Dir 指令显示曲面或网格的法线方向,正常的实体物件的法线方向是朝外的。
这个网格的法线方向不一致。
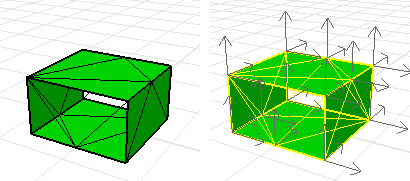
反转多重曲面上某些曲面的法线方向
| 1. | 使用 Explode 指令或 ExtractSrf 指令抽离法线方向不一致的曲面。 |
| 2. | 使用 Dir 指令反转个别曲面的法线方向。 |
| 3. | 使用 Join 指令将所有的曲面重新组合成多重曲面。 |
反转法线方向不正确的网格
| 4 | 使用 UnifyMeshNormals 指令。 修复后的网格的法线方向会朝着同一侧。
|
不同的学科或教科书在定义不同的力矩时可能使用不同 ( 甚至会互相冲突 ) 的术语和符号。在面积或体积力矩报告中的资讯可以用来计算任何其它力矩,为了获得您需要的力矩,您可能需要结合力矩报告中的几个数值。
范例
对角位于 0,0,0 和 6,10,0 的矩形平面 (Z 座标固定),其面积力矩报告如下:
面积 = 60 (+/- 1e-008)
面积重心 = 3,5,0 (+/- 1e-009,1e-009,0)
面积力矩:
First Moments
x: 180 (+/- 1e-007)
y: 300 (+/- 1e-007)
z: 0 (+/- 0)
Second Moments
xx: 720 (+/- 1e-007)
yy: 2000 (+/- 1e-006)
zz: 0 (+/- 0)
Product Moments
xy: 900 (+/- 1e-007)
yz: 0 (+/- 0)
zx: 0 (+/- 0)
Area Moments of Inertia about World Coordinate Axes
Ix: 2000 (+/- 1e-006)
Iy: 720 (+/- 1e-007)
Iz: 2720 (+/- 1e-006)
Area Radii of Gyration about World Coordinate Axes
Rx: 5.77350269 (+/- 1e-009)
Ry: 3.46410162 (+/- 1e-009)
Rz: 6.73300329 (+/- 1e-009)
Area Moments of Inertia about Centroid Coordinate Axes
Ix: 500 (+/- 1e-007)
Iy: 180 (+/- 1e-007)
Iz: 680 (+/- 1e-007)
Area Radii of Gyration about Centroid Coordinate Axes
Rx: 2.88675135 (+/- 1e-009)
Ry: 1.73205081 (+/- 1e-009)
Rz: 3.36650165 (+/- 1e-009)
括弧中的数字表示计算的精确度。
面积和体积力矩报告中的数值的详细叙述如下:
一次力矩
面积一次力矩的单位是长度3,体积一次力矩的单位是长度4。讨论 XY 平面的面积力矩时,Mx 在一些教科书中是代表"一次力矩 y:"的数值,而在另外一些教科书中是代表"一次力矩 x:"的数值,这种令人困扰的情形同样也发生在 My。
以积分而言,面积一次力矩的定义如下:
面积一次力矩 x:值 = 面积积分 x dA,
面积一次力矩 y:值 = 面积积分 y dA,
面积一次力矩 z:值 = 面积积分 z dA,
类似地,体积一次力矩的定义如下:
体积一次力矩 x:值 = 体积积分 x dV,
体积一次力矩 y:值 = 体积积分 y dV,
体积一次力矩 z:值 = 体积积分 z dV,
对面积或体积而言,一次力矩与面积或体积及面积重心之间的关系是:
重心 x 座标 = ( 一次力矩 x:值 ) / M,
重心 y 座标 = ( 一次力矩 y:值 ) / M,
重心 z 座标 = ( 一次力矩 z:值 ) / M,
其中的 M 代表面积或体积。
二次力矩
面积二次力矩的单位是长度4,体积二次力矩的单位是长度5。
以积分而言,面积一次力矩的定义如下:
面积二次力矩 xx:值 = 面积积分 x2 dA,
面积二次力矩 yy:值 = 面积积分 y2 dA,
面积二次力矩 zz:值 = 面积积分 z2 dA,
类似地,体积二次力矩的定义如下:
体积二次力矩 xx:值 = 体积积分 x2 dV,
体积二次力矩 yy:值 = 体积积分 y2 dV,
体积二次力矩 zz:值 = 体积积分 z2 dV,
积力矩
面积的积力矩单位是长度4,体积的积力矩单位是长度5。
以积分而言,面积一次力矩的定义如下:
面积的积力矩 xy:值 = 面积积分 xy dA,
面积的积力矩 yz:值 = 面积积分 yz dA,
面积的积力矩 zx:值 = 面积积分 zx dA,
类似地,体积二次力矩的定义如下:
体积的积力矩 xy:值 = 体积积分 xy dV,
体积的积力矩 yz:值 = 体积积分 yz dV,
体积的积力矩 zx:值 = 体积积分 zx dV。
以面积或体积而言,惯性积在计算不与任一座标轴平行的轴惯性力矩时很有用。尤其是任何轴面积惯性力矩可以由面积、面积一次力矩及面积二次力矩的线性组合表示。
世界座标轴惯性力矩
面积惯性力矩的单位是长度4,体积惯性力矩的单位是长度5。一般标准是使用 Ix、 Iy 及 Iz 分別代表世界 x 轴、y 轴及 z 轴的面积惯性力矩。
以积分而言,世界座标轴的面积惯性力矩定义如下:
Ix= 面积积分 (y2+ z2) dA ,
Iy= 面积积分(z2+ x2) dA ,
Iz= 面积积分(x2+ y2) dA 。
体积惯性力矩也是以类似的方式定义。
对于面积或体积而言,世界座标轴惯性力矩根据二次力矩定义:
Ix = 二次力矩 yy: 值 + 二次力矩 zz: 值,
Iy = 二次力矩 zz: 值 + 二次力矩 xx: 值,
Iz = 二次力矩 xx: 值 + 二次力矩 yy: 值,
世界座标轴的回转半径
回转半径的单位是长度,工程参考资料和教科书常以 R 或 k 表示回转半径,3D 轴的面积回转半径定义为:(轴的面积惯性力矩) 的平方根 / 面积。
类似地,体积回转半径的定义为:(轴的体积惯性力矩) 的平方根 / 体积。
对于面积或体积而言,面积力矩报告中的世界座标轴回转半径的计算方式如下:
Rx = 平方根( Ix / M ),
Ry = 平方根( Iy / M ),
Rz = 平方根( Iz / M ),
其中的 M 代表面积或体积。
Ix、Iy 及 Iz 是世界座标轴的面积惯性力矩。
重心座标轴惯性力矩
重心的面积惯性力矩的单位是长度4,重心的体积惯性力矩的单位是长度5。一般标准是使用 Ix、Iy 及 Iz 代表面积惯性力矩。
以积分而言,物件面积重心的面积惯性力矩定义如下:
Ix = 面积积分 ((y-y0)2 +( z-z0)2) dA ,
Iy = 面积积分((z-z0)2 +( x-x0)2) dA ,
Iz = 面积积分((x-x02 + (y-y0)2) dA ,
其中(x0>, y0, z0) 是面积重心。
体积重心的体积惯性力矩也是以类似的方式定义。
重心的面积 ( 或体积 ) 惯性力矩是以二次力矩、一次力矩及面积 ( 或体积 ) 表示:
Ix = 二次力矩 yy: 值
+ 二次力矩 zz: 值
- 2*y0*(一次力矩 y: 值)
- 2*z0*(一次力矩 z: 值)
+ (y02+z02)*M,
Iy = 二次力矩 zz: 值
+ 二次力矩 xx: 值
- 2*z0*(一次力矩 z: 值)
- 2*x0*(一次力矩 x: 值)
+ (y02+z02)*M,
Iz = 二次力矩 xx: 值
+ 二次力矩 yy: 值
- 2*x0*(一次力矩 x: 值)
- 2*y0*(一次力矩 y: 值)
+ (x02+y02) *M,
其中的 M 代表面积或体积。
重心座标轴的回转半径
重心回转半径的单位是长度,就面积或体积而言,在力矩报告中的重心回转半径的计算方式如下:
Rx = 平方根 ( Ix / M ),
Ry = 平方根 ( Iy / M ),
Rz = 平方根 ( Iz / M ),
其中的 M 代表面积或体积。
这里的 Ix、Iy 及 Iz 是面积重心惯性力矩或体积重心惯性力矩。