CurvatureAnalysis 指令使用假色分析曲面的曲率。
附注
| ● | 这些工具可以显示曲面的各种类形的曲率资讯,高斯曲率与平均曲率可以看出曲面的形状是否正常。 |
| ● | 可以找出曲面形状不正常的位置,例如:突起、凹洞、平坦、波浪状或曲面的某个部分的曲率大于或小于周围,必要时可以对曲面形状做修正。 |
| ● | 高斯曲率可以协助判断一个曲面是否可以展开为平面。 |
| ● | 光滑曲面上的任何一点都有两个主曲率,高斯曲率是这两个主曲率的乘积,平均曲率是这两个主曲率的平均数。 |
附注
| ● | 如果您要使用 CurvatureAnalysis 指令分析的曲面没有分析网格存在,Rhino 会以 网格选项对话框中的设置建立在工作视窗中不可见的分析网格。 |
| ● | 曲面分析网格会储存在 Rhino 的文件里,这些网格可能会让文件变的很大。RefreshShade 指令与 Save、SaveAs 指令的仅储存几何图形选项可以清除文件中的分析网格。 |
| ● | 分析自由造型的 NURBS 曲面时,必需使用较精细的网格才可以得到较准确的分析结果。 |
曲率
型式
高斯
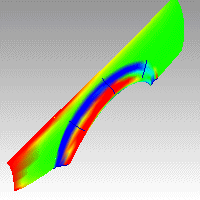
在以下的几个图例中,红色部分的高斯曲率为正数,绿色部分为 0,蓝色部分为负数。
曲面上的每一个点都会以您设定的曲率范围渐层颜色显示。例如,曲率位于曲率范围中间的曲面会以绿色显示,曲率超出红色范围的会以红色显示,曲率超出蓝色范围的会以蓝色显示。
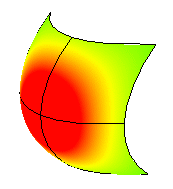
正曲率
高斯曲率为正,代表曲面的形状为碗形。
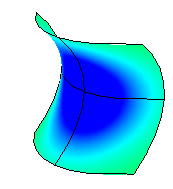
负曲率
高斯曲率为负,代表曲面的形状为马鞍型。
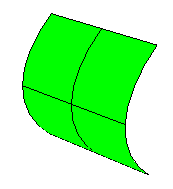
0 曲率
曲率为 0,代表曲面至少有一个方向是直的。例如:平面、圆柱体侧面、圆锥体侧面的高斯曲率都是 0。
如果您对某个曲率范围感兴趣,可以在曲率分析对话框中的"彩虹条"两端的栏位输入两个不同的数值,红色的数值未必一定要大于蓝色的数值。
平均
显示平均曲率的绝对值,适用于找出曲面曲率变化较大的部分。
最小半径
如果您想将曲面偏移一个特定距离 r,或使用半径为 r 的球状刀具加工,曲面上任何半径小于 r 的部分将会发生问题。
曲面上半径小于偏移距离的部分在曲面偏移后会发生自交,小于加工时使用的球状刀具的半径时,刀具可能会车除应该被保留的部分。
为避免发生这些问题,您可能会想问:这个曲面有任何部分的半径太小吗?最小半径可以为您解答这个问题。
设定 红色 = r、蓝色 = 1.5 x r
曲面上的红色区域是在偏移或加工时一定会发生问题部分,蓝色区域为安全的部分,绿色与红色之间的渐层区域为可能发生问题的部分。
最大半径
这个选项适用于找出曲面较平坦的部分。将蓝色的数值设得大一点 (10 -> 100 -> 1000),红色的数值设为接近无限大,曲面上红色的区域为近似平面的部分,曲率几乎等于 0。
曲率范围
CurvatureAnalysis 指令会将假色以曲率值对应至曲面上。先以自动范围设定曲率范围,再调整曲率范围的两个数值使它比自动范围更能突显分析目的。
CurvatureAnalysis 指令会记住您上次分析曲面时所使用的设定及曲率范围。如果物件的形状有较大的改变或分析的是不同的物件,记住的设定值可能并不适用。遇到这种情形时,您可以使用自动范围,让指令自动计算曲率范围,得到较好的对应颜色分布。
您可以使用最大范围将红色对应至曲面上曲率最大的部分,将蓝色对应至曲面上曲率最小的部分。当曲面的曲率有剧烈的变化时,产生的结果可能没有参考价值。
 显示结构线
显示结构线
显示物件上的结构线
为增选的物件显示曲率分析。
关闭增选物件的曲率分析。
要了解曲面上一个点的高斯曲率必需先知道什么是曲线的曲率。
曲线上的任何一点都有一条与该点正切的直线,我们也可以找出与该点正切的圆,这个圆的半径倒数是曲线在该点的曲率。
曲线上某一点的正切圆有可能位于曲线的左侧或右侧,为了做区分,我可以将曲率加上正负符号,正切圆位于曲线左侧时曲率为正数,位于曲线右侧时曲率为负数,这种表示方式称为有正负的曲率。
正截面曲率是一个最广泛的曲面曲率的表示方式。以一个平面通曲面上的某一点切割曲面时会产生一条断面线,断面线上该点的曲率为曲面该点的曲率之一,这个曲率是有正负的曲率。
以许多不同方向的平面切过曲面上的同一点,会产生许多断面线,每一条断面线在该点的曲率都不同,其中必定有一个最大值和最小值。
高斯曲率
高斯曲率是曲面上一个点的最大主要曲率与最小主要曲率的乘积。高斯曲率为正数时,代表曲面上该点的最大主要曲率与最小主要曲率的断面线往曲面的同一侧弯曲。高斯曲率为负数时,最大主要曲率与最小主要曲率的断面线往曲面的不同侧弯曲。高斯曲率为 0 时,最大主要曲率与最小主要曲率的的断面线之一是直的 (曲率为 0)。
主要曲率
曲面上一个点的最大曲率和最小曲率称为主要曲率,高斯曲率和平均曲率都是由最大主要曲率与最小主要曲率计算而来。
平均曲率
平均曲率是曲面上一个点的最大主要曲率与最小主要曲率的平均数,曲面上一个点的平均曲率为 0 时,该点的高斯曲率可能是负数或 0。
一个曲面上任意点的平均曲率都是 0 的曲面称为极小曲面 (Minimal Surface)。一个曲面上任意点的平均曲率都是固定的曲面称为定值平均曲率 (Constant Mean Curvature, CMC) 曲面。
CMC 曲面上任意点的平均曲率都一样。
肥皂泡 (不论是漂浮在空中或附着在物件上) 是 CMC 曲面的一个例子。肥皂泡 (非肥皂膜) 包含着一个封闭空间,肥皂泡内部的压力比外部的压力要大一些,但由肥皂泡的表面张力所平衡,达成内外均衡。
极小曲面是属于 CMC 曲面的一种,曲面上的任意点的曲率都是 0。
附着于铁丝圈上的肥皂膜是极小曲面的一个例子,因为肥皂膜两侧的压力相同,肥皂膜不会因为气压而变形,使肥皂膜的表面积最小化。这种情形和肥皂泡不同,肥皂泡包含着固定量的空气,但内外压力不同。
CurvatureAnalysisOff 指令关闭曲率分析显示。
请参考