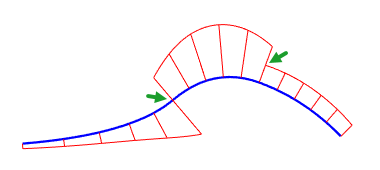
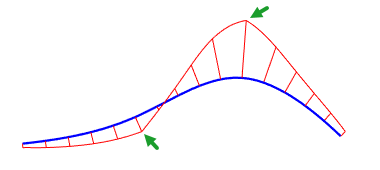
曲率の測定
Curvature
| ツールバー | メニュー |
|---|---|
|
|
解析 曲率分析(位置指定) |
Curvatureコマンドは、曲線またはサーフェス上の指定した点での曲率の値を円の半径を使用して評価します。
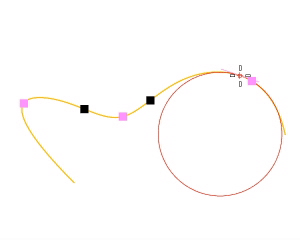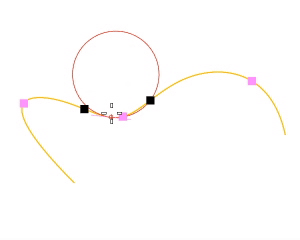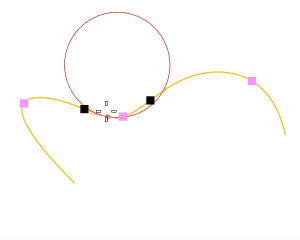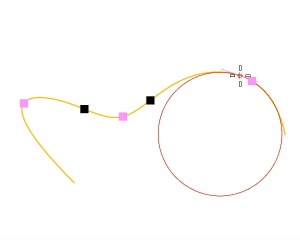
操作手順
サーフェスの曲率を分析するには
- サーフェスを選択します。
カーソルを動かすとカーソルの位置に2つの半円が現れ、その点での最小と最大の曲率を示します。 - サーフェス上の点をピックします。
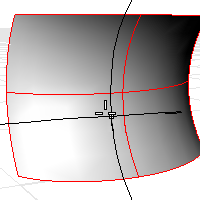
次のサーフェス評価情報がコマンド領域に表示されます。
- パラメータ位置でのサーフェス曲率評価
- 3D点
- 3D 法線
- 最大および最小主曲率
- ガウス曲率
- 平均曲率
メモ
- 滑らかな曲線上にあるすべての点には、その曲線のその地点での曲率を最も正確に近似した円があります。
- カーソルは自動的に曲線の変曲点(曲率の正、負が変わるところ)にスナップします。
- 同様に、滑らかなサーフェスにあるすべての点にも2つの曲率近似の円があります。半径が一番大きい円は半径が一番小さい円と直交します。
- 主曲率円弧の半径の逆数です。
- ガウス曲率は、両方の半円が同じ方向を向いている場合は正の値で、反対方向を向いている場合は負の値になります。一方の半円が直線の場合、ガウス曲率は0になります。
コマンドラインオプション
曲率カーブ作成
点オブジェクトと、曲率の円(曲線の場合)または曲率の半円(サーフェスの場合)をピックした点で作成します。
曲率半径が無限大の場合(曲率が0。曲線が局部的に平らである。例えば、曲線の湾曲が急激に反対に変わる変曲点など。)、それを知らせるメッセージが表示され、曲率は評価されません。これによって自動的に変曲点を見つけることはできませんが、手動で印を付けることができます。
| ツールバー | メニュー |
|---|---|
|
|
解析 サーフェス > 曲率分析 |
CurvatureAnalysisコマンドは、擬似カラー分析を用いてサーフェスの曲率を視覚的に評価します。疑似カラーはレイトレース以外のすべての表示モードで表示されます。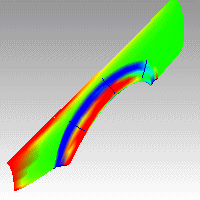
メモ
- これらのツールは、サーフェス上の曲率の種類や量についての情報を得るのに用いることができます。ガウスおよび平均曲率分析は、サーフェスの曲率に異常があった場合に、それを表示することができます。
- 受け入れられないような急な変化(突出した、へこんだ、平らな、または波状の部分や、周辺のサーフェスよりも曲率が高いまたは低い部分)の位置の確認をしたり、必要ならば修正したりということが行えます。
- ガウス曲率表示は、サーフェスが平らなパターンに展開できるのかどうかを決定するのに役に立ちます。
- 滑らかなサーフェスには2つの主曲率があります。ガウス曲率は、主曲率の積です。平均曲率は、2つの主曲率の平均です。
操作手順
- オブジェクトを選択します。
選択されたサーフェスはデフォルトではガウス曲率で解析されます。 - スタイルと範囲を設定します。
メモ
- CurvatureAnalysisコマンドを使用する際、選択したオブジェクトにサーフェス解析メッシュがない場合、ポリゴンメッシュオプションダイアログボックスの設定に基づいて見えないメッシュが作成されます。
- サーフェス解析メッシュはモデルと共にRhinoファイルに保存されます。このメッシュのサイズが大きくなる場合があります。この場合、RefreshShadeコマンド、そしてSave、SaveAsコマンドのジオメトリのみを保存オプションを使用すると、既存のサーフェス解析メッシュを削除することができます。
- 通常、分析コマンドを使ってフリーフォームのNURBSサーフェスを適切に分析するためには密度の高いメッシュが必要です。
曲率オプション
スタイル
ガウス
下のイメージで、赤はガウス曲率が正の部分を、緑はガウス曲率が0の部分を、そして青はガウス曲率が負の部分を表します。
指定した曲率の値の間にある値を持つサーフェス上の点は、その値に対応した色で表示されます。例えば、曲率の値が指定の値の中間の値を持つ点は、緑で表示されます。赤の範囲外の曲率の値を持つサーフェス上の点は赤で表示され、青の範囲外の曲率の値を持つサーフェス上の点は青で表示されます。
曲率が正の場合
ガウス曲率が正の場合、サーフェスは鉢形です。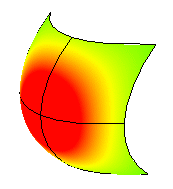
曲率が負の場合
負の場合、サーフェスは鞍形です。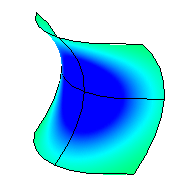
曲率が0の場合
0の場合、サーフェスが少なくとも1つの方向に平らであることを意味します。(平面、円柱、円錐体等はガウス曲率がゼロです。)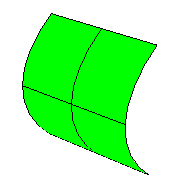
分析したい曲率の値の範囲が分かっている場合、その値を「虹」の赤と青の部分の横の編集ボックスに入力します。赤の値と青の値は異なる値でなければなりませんが、赤の値は青の値より大きくても小さくても構いません。
平均
平均曲率の絶対値を表示します。サーフェスの曲率が急に変化する部分を見つけるのに便利です。
最小半径
サーフェスをrの距離でオフセットする場合、またはサーフェスを半径がrのボールで切削加工する場合、サーフェスがrより小さい半径で「曲がる」部分には問題が発生します。
オフセットの場合、自己交差する曲がりくねったオブジェクトができてしまいます。切削加工の場合、ボールが残して置きたいマテリアルまで切り取ってしまいます。
このような場合、サーフェスが小さい半径で曲がる部分がないかどうかを見つけることが必要です。最小半径オプションはこのような場合に役に立ちます。
赤 = r、青 = 1.5 x rに設定します。
サーフェスの赤い部分はオフセットあるいは切削ができない部分です。青い部分は問題はないはずです。緑から赤に近い部分は気を付ける必要があります。
最大半径
このオプションは平らな部分を探し出すのに役に立ちます。青色の値を比較的高く設定し(10‑>100‑>1000)、赤色は無限大に近く設定します。こうすることにより、曲率の値が事実上0になる平らな部分が赤くなります。
曲率範囲
CurvatureAnalysisコマンドは、擬似カラー(フォルスカラー)を使用してサーフェスの曲率を分析します。このコマンドを使用するには、コンピュータの純色に値を割り当てる必要がありますが、まず自動範囲を使用すれば、2つの値を自動的に設定した後に、それらを対称に、しかも自動範囲が選択した範囲と同程度の範囲で調整することができます。
CurvatureAnalysisコマンドは、前回サーフェス分析を行った時の設定を使用します。しかし、サーフェスのジオメトリを著しく変更した場合や新しいサーフェスを分析しようとしている場合、前回の設定が適切ではない場合があるかもしれません。このような場合には、自動範囲オプションを使うと、曲率の違いが分かりやすい色の分布が得られるように曲率と色の対応マッピングを自動的に計算できます。
最大曲率を赤に、最小曲率を青にマップしたい場合、この最大範囲オプションを使用します。しかし、極端に曲率が変化するようなサーフェスの場合、このオプションのイメージはあまりよい情報を提供しない場合があります。
 エッジとアイソカーブを表示
エッジとアイソカーブを表示
分析するオブジェクト上にエッジまたはアイソカーブを表示します。
| ツールバー | メニュー |
|---|---|
|
|
|
CurvatureAnalysisOffコマンドは、曲率ダイアログボックスを閉じ、曲率分析表示をオフにします。
| ツールバー | メニュー | エイリアス |
|---|---|---|
|
|
解析 曲線 > 曲率表示オン |
COn |
CurvatureGraphコマンドは、曲線やサーフェスの曲率を図(グラフ)を用いて視覚的に評価します。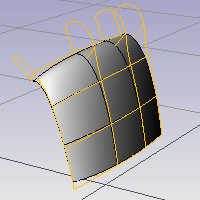
操作手順
| スパンの連続性 | |
|---|---|
|
接線連続 |
曲線スパンはそれぞれお互いに接線連続ですが、曲率表示はある値から急に異なる値に変わっています。次数2の曲線のスパンはG1で、接線連続のみです。曲率連続ではありません。 3つのスパンがある次数2の曲線。曲率のグラフはスパン間で急に変化します。
|
|
曲率連続 |
曲率表示で、値が急に変わっている部分はありません。1つ目のスパンの曲率表示の端と2つ目のスパンの曲率表示の端がきちんと合っています。スパンが接するところで曲率の値が急に変わっていないことから、この曲線の連続性はG2で、曲率連続です。しかし、1つ目のスパンの曲率表示の変化の度合いは2つ目のスパンの曲率の変化の度合いと異なります。曲率は同じですが、曲率の変化の率は急に変わっています。 3つのスパンがある次数3の曲線。曲率のグラフはスパン間で端と端が繋がっています。
|
Curvatureコマンドを使用して、曲線に沿って表示される円の動きを見てみると連続性が理解しやすくなるでしょう。
メモ
- サーフェスの場合、曲率マークはサーフェスのアイソパラメトリック曲線にしか表示されません。アイソパラメトリック曲線の表示がオフになっている場合、曲率マークはサーフェス境界にしか表示されません。
- 曲線(直線以外)のどの点においても、その点での曲率を一番正確に近似する円があります。これは、どの点においても同じ接線方向と接線方向の同じ変化率を持つ円があるということです。表示される曲率はその円を元に計算されたグラフで、式は(1 / 円の半径)です。スケールはダイアログボックスで設定される係数で調整されます。グラフが滑らかに変化する場合、曲線はスムーズ(滑らか)またはフェア(整形された)といいます。グラフに急に変化する部分がある場合、曲線の元の導関数にキンクまた急な変化があることを示します。
曲率表示のオプション
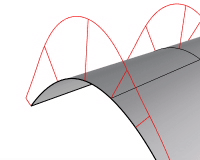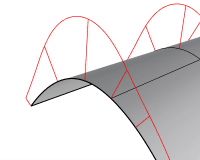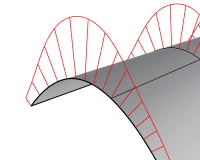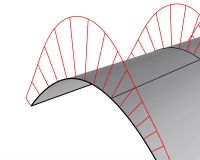
表示スケール
曲率表示の線のサイズを設定します。変化のスケールを強調することができます。曲率の変化が非常に微妙で分かりにくい場合、このオプションを使用してください。表示スケールが100の場合、スケール(尺度)は1:1を意味します。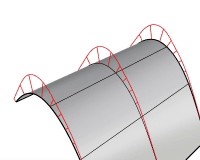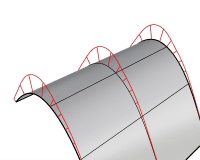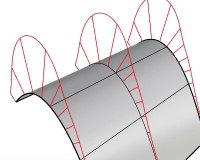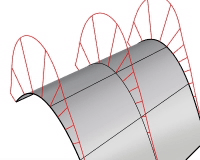
密度
曲率表示の線の数を設定します。
数
サーフェスの場合のみサーフェス上に表示される曲率グラフの数を制御します。
NURBSサーフェスのアイソカーブまたはSubDワイヤの数は、曲率グラフが常に表示されるように一時的に調整されます。
曲線マーク
曲線マークの色を設定するには
- 色ボタンをクリックして、曲線の曲率表示の色を設定します。
サーフェスマーク
サーフェスマークの色を設定するには
- 色ボタンをクリックして、サーフェスの曲率表示の色を設定します。
 U
U
U方向のみのサーフェスマークを表示します。
マークの色は色見本で設定できます。
 V
V
V方向のみのサーフェスマークを表示します。
マークの色は色見本で設定できます。
選択して追加するオブジェクトの曲率表示分析をオンにします。
選択するオブジェクトの曲率表示分析をオフにします。
| ツールバー | メニュー | エイリアス |
|---|---|---|
|
|
解析 曲線 > 曲率表示オフ |
COff |
CurvatureGraphOffコマンドは、曲率表示をオフにします。
曲線の曲率
サーフェス上の点におけるガウス曲率を理解するには、まず曲線の曲率について理解しなければなりません。
平面上の曲線のどの点をとってみても、その点を通り、その点で曲線を最もよく近似する線を接線と呼びます。また、曲線に接し、その点を通る形状を最もよく近似する円を求めることもできます。この円の半径の逆数がその点における曲線の曲率です
曲線を最もよく近似する円は曲線の右側にある場合も左側にある場合もあります。この区別が重要な場合は、慣例として円が左側にある場合はその曲率を正の曲率とみなし、右側にある場合は負の曲率とみなします。これが正負の符号のついた曲率ということになります。
曲率を一般化してサーフェスにも当てはめる概念として法曲率があります(英語でnormal section curvature、法断面曲率ともいいます)。サーフェス上の点、その点を通る接触平面、そしてその平面上に特定の方向にその点から伸びる線を考えてみましょう。点、方向、そしてその点でのサーフェスの法線で定義する平面がサーフェスと交差するところで断面曲線が定義されます。分析したい点でのこの曲線の正または負の曲率が法曲率です。
分析したいサーフェス上の点の接触平面のあらゆる方向での法曲率を計算すれば、最大値と最小値が必ずあります。
サーフェスの曲率
ガウス曲率
サーフェス上の点におけるガウス曲率はその点での主曲率の積です。正のガウス曲率がある点での接触平面はサーフェスと1 点でしか接触しませんが、負のガウス曲率がある点での接触平面はサーフェスを分割します。平均曲率がゼロの点はガウス曲率の値がゼロか負の値です。
主曲率
特定の点における法曲率の最大値と最小値はサーフェスのその点における主曲率です。(法曲率は特定の点からの接線ベクトルと法線で定義される平面上にある、サーフェス上の曲線の曲率です。)この主曲率はサーフェスのガウス曲率と平均曲率の計算に使用されます。
平均曲率
サーフェス上の点における平均曲率はその点での主曲率の和の半分です。平均曲率がゼロの点はガウス曲率の値がゼロか負の値です。
あらゆる点で平均曲率がゼロのサーフェスは極小曲面といいます。あらゆる点での平均曲率の値が一定しているサーフェスは平均曲率一定曲面(CMC - Constant Mean Curvature Surface)と呼ばれることもあります。
平均曲率一定曲面はあらゆる点での平均曲率の値が一定しています。
平均曲率一定曲面でモデリングできる物理的プロセスの例としてシャボン玉(自由に飛んでいる場合や何かにくっついている場合)があります。単純な石けん膜と違って、シャボン玉は体積を持ち、外部より多少高いシャボン玉の内部の圧力と、シャボン玉自体の表面積を最も小さくしようとする力が釣り合っている状態にあります。
極小曲面は至るところの曲率がゼロの平均曲率一定曲面の中のサブセットです。
極小曲面でモデリングできる物理的プロセスの例として、固定された枠(針金の輪など)に張っている石けん膜があります。石けん膜は空気圧で変形されず(どちらの側に対する圧力も同じなので)、表面積を最も小さくする妨げはありません。これは一定の空気の量を持っていて内側と外側からの圧力が違うシャボン玉とは対照的です。