Volume mass properties
The objects selected as part of the volume command must bound a volume. The simplest way to ensure this is to select solid objects (closed, manifold, and oriented with their normal direction pointing outward). However, there are cases where it is inconvenient to join objects into such a polysurface or mesh.
In these cases, volume mass properties can be computed from a collection of non-solid objects.
You are responsible for ensuring that:
- The objects enclose a volume.
- Each surface is on the boundary of the volume, not in its interior.
- The surface or mesh normal points outward away from the volume.
Steps
- Use the Dir command to check or modify the surface or mesh normal.

Six rectangular surfaces or mesh faces with the correct orientation define the volume of the box.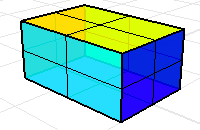
Without the top of the box the volume mass properties commands will return a meaningless result.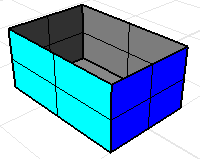

Volume mass properties of non-manifold objects
A polysurface or mesh for which every edge is shared by at most two faces is called a manifold. The volume mass property commands assume that every face bounds the volume.
A non-manifold polysurface where every surface does not bound a volume. The volume mass properties commands will give a meaningless answer.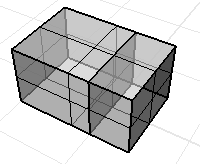
A non-manifold polysurface where every surface bounds a volume. The volume mass properties commands will return valid data.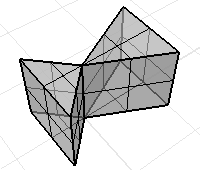
Volume mass properties of non-oriented objects
A polysurfaces or a mesh may have inconsistent orientations on the faces.
Use the Dir command to display the face normals. A properly oriented solid will have outward pointing normals.
This mesh has inconsistent normals.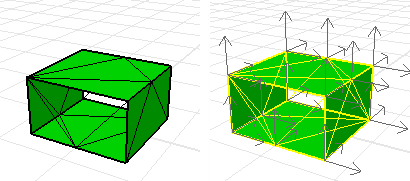
To change normals on some faces of a polysurface
- Use the Explode command or the ExtractSrf command to isolate the offending faces.
- Use the Dir command on individual faces to properly orient the normals.
- Use the Join command to reconstruct the polysurface.
To change normals on non-oriented meshes
- Use the UnifyMeshNormals command.
The fixed mesh with consistent, outward pointing normals.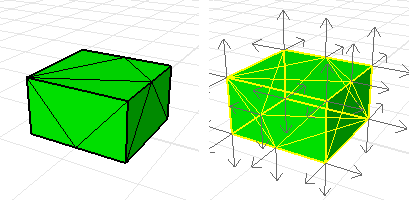
Mass properties calculation details
Different disciplines and textbooks use different, and sometimes contradictory, nomenclature and notation when defining various moments. The information in the area or volume moments report can be used to compute any of these moments. In order to get the particular moment you need, you may have to combine several of the values from the moments report.
Example
The area moments report for a constant z plane with corners at 0,0,0 and 6,10,0 is shown below.
Area = 60 (+/- 1e-008)
Area Centroid = 3,5,0 (+/- 1e-009,1e-009,0)
Area Moments:
First Moments
x: 180 (+/- 1e-007)
y: 300 (+/- 1e-007)
z: 0 (+/- 0)
Second Moments
xx: 720 (+/- 1e-007)
yy: 2000 (+/- 1e-006)
zz: 0 (+/- 0)
Product Moments
xy: 900 (+/- 1e-007)
yz: 0 (+/- 0)
zx: 0 (+/- 0)
Area Moments of Inertia about World Coordinate Axes
Ix: 2000 (+/- 1e-006)
Iy: 720 (+/- 1e-007)
Iz: 2720 (+/- 1e-006)
Area Radii of Gyration about World Coordinate Axes
Rx: 5.77350269 (+/- 1e-009)
Ry: 3.46410162 (+/- 1e-009)
Rz: 6.73300329 (+/- 1e-009)
Area Moments of Inertia about Centroid Coordinate Axes
Ix: 500 (+/- 1e-007)
Iy: 180 (+/- 1e-007)
Iz: 680 (+/- 1e-007)
Area Radii of Gyration about Centroid Coordinate Axes
Rx: 2.88675135 (+/- 1e-009)
Ry: 1.73205081 (+/- 1e-009)
Rz: 3.36650165 (+/- 1e-009)
The numbers shown in parenthesis report the accuracy of the computation.
Precise descriptions of the values in the area and volume moments report are given below.
First moments
The area first moments have units of length3. The volume first moments have units of length4. When discussing area moments in the xy plane, some disciplines and textbooks use the symbol Mx, to denote the value reported as "First Moments y:" while other disciplines and textbooks use the same symbol to denote the value reported as "First Moments x:". A similar confusing situation involves the symbol My.
In terms of integrals, the area first moments are defined by:
Area first moment x: value = integral of x dA over the area,
Area first moment y: value = integral of y dA over the area,
Area first moment z: value = integral of z dA over the area.
Similarly, the volume first moments are defined by:
Volume first moment x: value = integral of x dV over the volume,
Volume first moment y: value = integral of y dV over the volume,
Volume first moment z: value = integral of z dV over the volume.
For either an area or a volume, the relationship between the first moments, the area or volume, and the area centroid is:
Centroid x coordinate = (first moment x: value)/M,
Centroid y coordinate = (first moment y: value)/M,
Centroid z coordinate = (first moment z: value)/M,
where M is the area or volume.
Second moments
The area second moments have units of length4. The volume second moments have units of length5.
In terms of integrals, the area second moments are defined by:
Area second moment xx: value = integral of x2 dA over the area,
Area second moment yy: value = integral of y2 dA over the area,
Area second moment zz: value = integral of z2 dA over the area.
Similarly, volume second moments are defined by:
Volume second moment xx: value = integral of x2 dV over the volume,
Volume second moment yy: value = integral of y2 dV over the volume,
Volume second moment zz: value = integral of z2 dV over the volume.
Product moments
The area product moments have units of length4. The volume product moments have units of length5.
In terms of integrals, the area product moments are defined by:
Area product moment xy: value = integral of xy dA over the area,
Area product moment yz: value = integral of yz dA over the area,
Area product moment zx: value = integral of zx dA over the area.
Similarly, volume product moments are defined by:
Volume product moment xy: value = integral of xy dV over the volume,
Volume product moment yz: value = integral of yz dV over the volume,
Volume product moment zx: value = integral of zx dV over the volume.
For either an area or a volume, products of inertia are useful for computing moments of inertia about axes that are not parallel to a coordinate axis. In particular, an area moment of inertia about any axis can be expressed as a linear combination of the area, area first moments, area second moments, and area product moments.
Moments of inertia about world-coordinate axes
The area moments of inertia have units of length4. The volume moments of inertia have units of length5. It is fairly standard to use the symbols Ix, Iy, and Iz to denote the area moments of inertia about the world x axis, y axis, and z axis, respectively.
In terms of integrals, the area moments of inertia about the world axes are defined by:
Ix= integral of (y2+ z2) dA over the area,
Iy= integral of (z2+ x2) dA over the area,
Iz= integral of (x2+ y2) dA over the area.
Volume moments of inertia are defined in a similar manner.
For either an area or a volume, the moments of inertia about the world axes are defined in terms of second moments by:
Ix = second moment yy: value + second moment zz: value,
Iy = second moment zz: value + second moment xx: value,
Iz = second moment xx: value + second moment yy: value.
Radii of gyration about world-coordinate axes
The radii of gyration have units of length. Engineering references and textbooks frequently use R or k to denote radii of gyration. The area radius of gyration about a 3-D axis is defined to be the square root of (area moment of inertia about the axis)/area.
Similarly, the volume radius of gyration is defined as the square root of (volume moment of inertia about the axis)/volume.
For either an area or a volume, radii of gyration about the world axes in the area moments report are computed as:
Rx = sqrt( Ix / M ),
Ry = sqrt( Iy / M ),
Rz = sqrt( Iz / M ),
where M is the area or volume.
Here the Ix, Iy, and Iz are the area moments of inertia about the world axes.
Moments of inertia about centroid-coordinate axes
The area moments of inertia about the centroid have units of length4. The volume moments of inertia about the centroid have units of length5. It is also fairly standard to use the symbols Ix, Iy, and Iz to denote these area moments of inertia.
In terms of integrals, the area moments of inertia about the object's area centroid are defined by:
Ix = integral of ((y-y0)2+( z-z0)2 dA over the area,
Iy = integral of ((z-z0)2+( x-x0)2) dA over the area,
Iz = integral of ((x-x0)2+(y-y0)2) dA over the area,
Here (x0 > y0, z0) is the area centroid.
Volume moments of inertia about the volume centroid are defined in a similar manner.
The area (or volume) moments of inertia are expressed in terms second moments, first and volume):
Ix = second moment yy: value
+ second moment zz: value
- 2*y0*(first moment y: value)
- 2*z0*(first moment z: value)
+ (y02+z02)*M,
Iy = second moment zz: value
+ second moment xx: value
- 2*z0*(first moment z: value)
- 2*x0*(first moment x: value)
+ (z02+x02)*M,
Iz = second moment xx: value
+ second moment yy: value
- 2*x0*(first moment x: value)
- 2*y0*(first moment y: value)
+ (x02+y02) *M,
where M is the area or volume.
Radii of gyration about centroid-coordinate axes
The radii of gyration about the centroid have units of length. For an area or a volume, the radii of gyration about the centroid in the moments report are computed as:
Rx = sqrt( Ix / M ),
Ry = sqrt( Iy / M ),
Rz = sqrt( Iz / M ),
where M is the area or volume.
Here the Ix, Iy, and Iz are the area (or volume) moments of inertia about the area or volume centroid.
See also
AreaCentroid
Report and marks an object's area centroid.
AreaMoments
Report an object's area moments of inertia.
VolumeCentroid
Report the coordinates of and place a point object at the volume centroid of surfaces and polysurfaces.
VolumeMoments
Report the volume moments of inertia of surfaces and polysurfaces.