
Die Objekte, die als Teil des Befehls Volumen ausgewählt wurden, müssen ein Volumen einschließen. Dies kann am einfachsten garantiert werden, wenn Sie die soliden Objekte auswählen (geschlossen, mannigfaltig und mit ihrer Normalenrichtung nach außen gerichtet). Es gibt jedoch Fälle, in denen es mühsam ist, Objekte zu einem Flächenverband oder Polygonnetz zu verbinden.
In diesen Fällen können Masseeigenschaften des Volumens aus einer Sammlung nicht-solider Objekte berechnet werden.
Sie sind dafür zuständig, dass:
| ● | Die Objekte ein Volumen umschließen. |
| ● | Jede Fläche sich auf der Begrenzung des Volumens befindet, nicht innerhalb. |
| ● | Die Flächen- oder Polygonnetznormalenpunkte nach außen, weg vom Volumen gerichtet sind. |
Vorgehen
Verwenden Sie den Befehl Richtung, um die Flächen- oder Polygonnetznormalen zu überprüfen oder ändern.

Sechs rechteckige Flächen oder Polygonnetzseiten mit der richtigen Ausrichtung definieren das Volumen des Quaders.
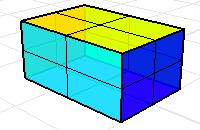
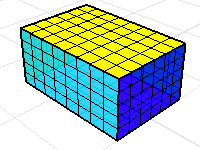
Ohne den oberen Teil des Quaders werden die Masseeigenschaften des Volumens bedeutungslose Resultate liefern.
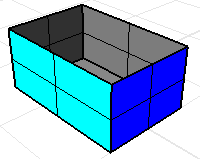

Ein Flächenverband oder Polygonnetz, dessen Kanten alle maximal zwei Seiten gemeinsam haben, nennt man mannigfaltig. Die Befehle der Volumenmasseeigenschaften setzen voraus, dass alle Seiten das Volumen einschließen.
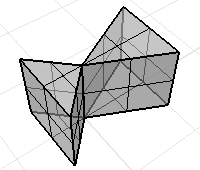
Nicht-mannigfaltiger Flächenverband, bei dem keine Fläche ein Volumen einschließt. Die Befehle der Volumenmasseeigenschaften bieten bedeutungslose Antworten.
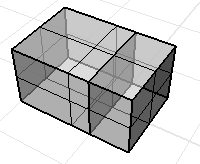
Nicht-mannigfaltiger Flächenverband, bei dem jede Fläche ein Volumen einschließt. Die Befehle der Volumenmasseeigenschaften liefern gültige Daten.
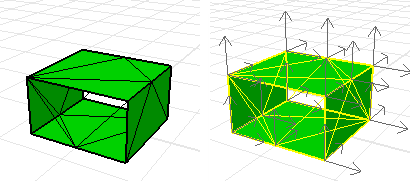
Ein Flächenverband oder Polygonnetz kann inkonsistente Ausrichtungen auf den Seiten aufweisen.
Verwenden Sie den Befehl Richtung, um die Seitennormalen anzuzeigen. Die Normalen eines richtig ausgerichteten Volumenkörpers zeigen nach außen.
Dieses Polygonnetz hat inkonsistente Normalen.
Die Normalen auf einigen Seiten eines Flächenverbands ändern
| 1. | Verwenden Sie den Befehl Zerlegen oder FlächeLösen, um die fehlerhaften Seiten zu isolieren. |
| 2. | Verwenden Sie den Befehl Richtung an einzelnen Seiten, um die Normalenrichtig auszurichten. |
| 3. | Verwenden Sie den Befehl Verbinden, um den Flächenverband neu zu erzeugen. |
Die Normalen auf nicht-ausgerichteten Polygonnetzen ändern
Verwenden Sie den Befehl PolygonnetzNormalenVereinheitlichen.
Das reparierte Polygonntez mit konsistenten, nach außen gerichteten Normalen.
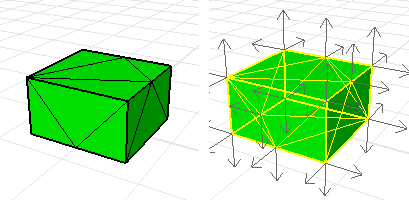
Verschiedene Disziplinen und Textbücher verwenden verschiedene und manchmal widersprüchliche Nomenklatur und Bezeichnung bei der Definition verschiedener Momente. Die Information in der Flächen- oder Volumentmomentanzeige kann zur Berechnung dieser Momente verwendet werden. Um das gewünschte Moment zu erhalten, müssen Sie vielleicht verschiedene Werte der Momentanzeige kombinieren.
Beispiel
Die Flächenmomente für eine konstante Z-Ebene mit Eckpunkten bei 0,0,0 und 6,10,0 werden unten angezeigt.
Flächeninhalt = 60 (+/- 1e-008)
Flächenmittelpunkt = 3,5,0 (+/- 1e-009,1e-009,0)
Flächenmomente:
Momente erster Ordnung
x: 180 (+/- 1e-007)
y: 300 (+/- 1e-007)
z: 0 (+/- 0)
Momente zweiter Ordnung
xx: 720 (+/- 1e-007)
yy: 2000 (+/- 1e-006)
zz: 0 (+/- 0)
Produktmomente
xy: 900 (+/- 1e-007)
yz: 0 (+/- 0)
zx: 0 (+/- 0)
Trägheitsmomente im Verhältnis zu den Welt-Koordinatenachsen
Ix: 2000 (+/- 1e-006)
Iy: 720 (+/- 1e-007)
Iz: 2720 (+/- 1e-006)
Kreisradien im Verhältnis zu den Welt-Koordinatenachsen
Rx: 5.77350269 (+/- 1e-009)
Ry: 3.46410162 (+/- 1e-009)
Rz: 6.73300329 (+/- 1e-009)
Trägheitsmomente im Verhältnis zu den Koordinatenachsen des Mittelpunkts
Ix: 500 (+/- 1e-007)
Iy: 180 (+/- 1e-007)
Iz: 680 (+/- 1e-007)
Kreisradien im Verhältnis zu den Koordinatenachsen des Mittelpunkts
Rx: 2.88675135 (+/- 1e-009)
Ry: 1.73205081 (+/- 1e-009)
Rz: 3.36650165 (+/- 1e-009)
Die Zahlen in Klammern zeigen die Genauigkeit der Berechnung an.
Genaue Beschreibungen der Werte in der Flächen- und Volumenmomentanzeige werden unten angezeigt.
Momente erster Ordnung
Die Flächenmomente erster Ordnung besitzen Längeneinheiten von 3. Die Volumenmomente erster Ordnung besitzen Längeneinheiten von 4. Wenn Flächenmomente in der XY-Ebene erörtert werden, verwenden einige Disziplinen und Textbücher das Symbol Mx, um den als "Momente erster Ordnung y:" angezeigten Wert zu kennzeichnen, während andere Disziplinen und Textbücher das gleiche Symbol verwenden, um den als "Momente erster Ordnung x:" angezeigten Wert zu markieren. Eine ähnlich verwirrende Situation betrifft das Symbol My.
Was Integrale betrifft, werden die Trägheitsmomente der Fläche im Verhältnis zu den Weltachsen definiert durch:
Flächenmoment erster Ordnung x: Wert = Integral von x dA über der Fläche,
Flächenmoment erster Ordnung y: Wert = Integral von y dA über der Fläche,
Flächenmoment erster Ordnung z: Wert = Integral von z dA über der Fläche.
Die Flächenmomente erster Ordnung werden definiert durch:
Volumenmoment erster Ordnung x: Wert = Integral von x dV über dem Volumen,
Volumenmoment erster Ordnung y: Wert = Integral von y dV über dem Volumen,
Volumenmoment erster Ordnung z: Wert = Integral von z dV über dem Volumen.
Für Fläche oder auch Volumen ist die Beziehung zwischen den Momenten erster Ordnung, Fläche und Volumen, und dem Flächenmittelpunkt:
Mittelpunkt x Koordinate = (Moment erster Ordnung x: Wert)/M,
Mittelpunkt y Koordinate = (Moment erster Ordnung y: Wert)/M,
Mittelpunkt z Koordinate = (Moment erster Ordnung z: Wert)/M,
wobei M Fläche oder Volumen ist.
Momente zweiter Ordnung
Die Flächenmomente zweiter Ordnung besitzen Längeneinheiten von 4. Die Trägheitsmomente des Volumens im Verhältnis zum Mittelpunkt besitzen Längeneinheiten von 5.
Was Integrale betrifft, werden die Trägheitsmomente der Fläche im Verhältnis zu den Weltachsen definiert durch:
Flächenmoment zweiter Ordnung xx: Wert = Integral von x2 dA über der Fläche,
Flächenmoment zweiter Ordnung yy : Wert = Integral von y2 dA über der Fläche,
Flächenmoment zweiter Ordnung zz: Wert = Integral von z2 dA über der Fläche.
Die Volumenmomente zweiter Ordnung werden definiert durch:
Volumenmoment zweiter Ordnung xx: Wert = Integral von x2 dV über dem Volumen,
Volumenmoment zweiter Ordnung yy: Wert = Integral von y2 dV über dem Volumen,
Volumenmoment zweiter Ordnung zz: Wert = Integral von z2 dV über dem Volumen.
Produktmomente
Die Flächenproduktmomente besitzen Längeneinheiten von 4. Die Trägheitsmomente des Volumens im Verhältnis zum Mittelpunkt besitzen Längeneinheiten von 5.
Was Integrale betrifft, werden die Trägheitsmomente der Fläche im Verhältnis zu den Weltachsen definiert durch:
Flächenproduktmoment xy: Wert = Integral von xy dA über der Fläche,
Flächenproduktmoment yz: Wert = Integral von yz dA über der Fläche,
Flächenproduktmoment zx: Wert = Integral von zx dA über der Fläche.
Die Volumenproduktmomente werden definiert durch:
Volumenproduktmoment xy: Wert = Integral von xy dV über dem Volumen,
Volumenproduktmoment yz: Wert = Integral von yz dV über dem Volumen,
Volumenproduktmoment zx: Wert = Integral von zx dV über dem Volumen.
Für Fläche oder Volumen sind Trägheitsprodukte hilfreich für die Berechnung von Trägheitsmomenten im Verhältnis zu Achsen, die sich nicht parallel zu einer Koordinatenachse befinden. Ein Trägheitsmoment der Fläche im Verhältnis zu einer Achse kann als lineare Kombination der Fläche, der Flächenmomente erster Ordnung, der Flächenmomente zweiter Ordnung und der Produktmomente der Fläche ausgedrückt werden.
Trägheitsmomente im Verhältnis zu den Welt-Koordinatenachsen
Die Trägheitsmomente des Volumens im Verhältnis zum Mittelpunkt besitzen Längeneinheiten von 4. Die Trägheitsmomente des Volumens im Verhältnis zum Mittelpunkt besitzen Längeneinheiten von 5. Normalerweise werden die Symbole Ix, Iy und Iz verwendet, um die Trägheitsmomente der Fläche im Verhältnis zu den Welt-X-, Y- und Z-Achsen zu bezeichnen.
Was Integrale betrifft, werden die Trägheitsmomente der Fläche im Verhältnis zu den Weltachsen definiert durch:
Ix = Integral von (y2 + z2) dA über dem Flächeninhalt
Iy= Integral von (z2+ x2) dA über dem Flächeninhalt,
Iz = Integral von (x2 + y2) dA über der Fläche.
Trägheitsmomente des Volumens um den Volumenmittelpunkt werden ähnlich definiert.
Für Fläche oder Volumen werden die Trägheitsmomente im Verhältnis zu den Weltachsen definiert durch:
Ix = Moment zweiter Ordnung yy: Wert + Moment zweiter Ordnung zz: Wert,
Iy = Moment zweiter Ordnung zz: Wert + Moment zweiter Ordnung xx: Wert,
Iz = Moment zweiter Ordnung xx: Wert + Moment zweiter Ordnung yy: Wert.
Kreisradien im Verhältnis zu den Welt-Koordinatenachsen
Die Kreisradien besitzen Längeneinheiten. Referenzen im Ingenieurwesen und Textbücher verwenden oft R oder k, um Kreisradien zu bezeichnen. Ähnlich wird der Kreisradius des Volumens definiert als Quadratwurzel von (Trägheitsmoment des Volumens im Verhältnis zur Achse)/Volumen.
Ähnlich wird der Kreisradius des Volumens definiert als Quadratwurzel von (Trägheitsmoment des Volumens im Verhältnis zur Achse)/Volumen.
Für Fläche oder Volumen werden die Kreisradien im Verhältnis zu den Weltachsen in der Flächenmomentanzeige wie folgt berechnet:
Rx = Quadratwurzel( Ix / M ),
Ry = Quadratwurzel( Iy / M ),
Rz = Quadratwurzel( Iz / M ),
wobei M der Flächeninhalt oder das Volumen ist.
Hier sind Ix, Iy und Iz die Trägheitsmomente der Fläche (oder des Volumens) im Verhältnis zum Flächen- oder Volumenmittelpunkt.
Trägheitsmomente im Verhältnis zu den Koordinatenachsen des Mittelpunkts
Die Trägheitsmomente des Volumens im Verhältnis zum Mittelpunkt besitzen Längeneinheiten von 4. Die Trägheitsmomente des Volumens im Verhältnis zum Mittelpunkt besitzen Längeneinheiten von 5. Normalerweise werden die Symbole Ix, Iy und Iz verwendet, um diese Trägheitsmomente der Fläche zu bezeichnen.
Was Integrale betrifft, werden die Trägheitsmomente der Fläche im Verhältnis zum Flächenmittelpunkt des Objekts definiert durch:
Ix = Integral von ((y-y0)2 +( z-z0)2) dA über dem Flächeninhalt,
Iy = Integral von ((z-z0)2 +( x-x0)2) dA über dem Flächeninhalt,
Iz = Integral von ((x-x02 + (y-y0)2) dA über dem Flächeninhalt,
Hier ist (x0>, y0, z0) der Flächenschwerpunkt.
Trägheitsmomente des Volumens um den Volumenmittelpunkt werden ähnlich definiert.
Die Trägheitsmomente der Fläche (oder des Volumens) werden im Sinne von zweiter Ordnung, erster Ordnung und Volumen ausgedrückt):
Ix = Moment zweiter Ordnung yy: Wert
+ Moment zweiter Ordnung zz: Wert
- 2*y0*(Moment erster Ordnung y: Wert)
- 2*z0*(Moment erster Ordnung z: Wert)
+ (y02+z02)*M,
Iy = Moment zweiter Ordnung zz: Wert
+ Moment zweiter Ordnung xx: Wert
- 2*z0*(Moment erster Ordnung z: Wert)
- 2*x0*(Moment erster Ordnung x: Wert)
+ (z02+x02)*M,
Iz = Moment zweiter Ordnung xx: Wert
+ Moment zweiter Ordnung yy: Wert
- 2*x0*(Moment erster Ordnung x: Wert)
- 2*y0*(Moment erster Ordnung y: Wert)
+ (x02+y02) *M,
wobei M Fläche oder Volumen ist.
Kreisradien im Verhältnis zu den Koordinatenachsen des Mittelpunkts
Die Trägheitsmomente des Volumens im Verhältnis zum Mittelpunkt besitzen Längeneinheiten von 5. Für Fläche oder Volumen werden die Kreisradien im Verhältnis zu den Weltachsen in der Momentanzeige wie folgt berechnet:
Rx = Quadratwurzel( Ix / M ),
Ry = Quadratwurzel( Iy / M ),
Rz = Quadratwurzel( Iz / M ),
wobei M der Flächeninhalt oder das Volumen ist.
Hier sind Ix, Iy und Iz die Trägheitsmomente der Fläche (oder des Volumens) im Verhältnis zum Flächen- oder Volumenschwerpunkt.
Rhino for Mac © 2010-2015 Robert McNeel & Associates. 31. August 2015