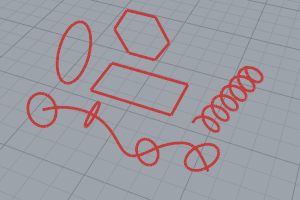
Una curva de Rhino es similar a una estructura alámbrica. Puede ser recta u ondulada, puede ser abierta o cerrada.
Una policurva es una curva formada por varios segmentos unidos de extremo a extremo.
Rhino ofrece varias herramientas para la creación de curvas. Se pueden dibujar líneas rectas, polilíneas formadas por segmentos de línea conectados, arcos, círculos, polígonos, elipses, hélices y espirales.
También puede dibujar curvas utilizando puntos de control de curvas y curvas que atraviesan los puntos seleccionados.
Véase: Wikipedia: Curva.
Esta curva es de grado 1 y no tiene pliegues. Una polilínea es una serie de segmentos de línea unidos.
Dibuja un solo segmento de línea.
Traza una línea a través de cualquier combinación de puntos, puntos de control y nubes de puntos.
Dibuja una polilínea de varios segmentos con las opciones segmentos de línea y arco, líneas auxiliares y cerrar.
Dibuja un polígono con un número específico de lados con las opciones inscrito/circunscrito, por borde, en forma de estrella, alrededor una curva y vertical.
Dibuja una polilínea cerrada rectangular con las opciones inicio en el centro, tres puntos, vertical y redondeada con arco o esquinas cónicas.
Véase: Wikipedia: Línea.
Las curvas de forma libre en Rhino son curvas NURBS. Una curva NURBS se define por su orden, un conjunto de puntos de control ponderados y un vector nodal.
Rhino ofrece varios métodos para crear curvas de forma libre.
Crea una curva que describe un cable o una cadena suspendida por sus dos extremos y que sostiene únicamente su propio peso.
Dibuja una curva a partir de posiciones de puntos de control.
Dibuja curvas Bézier en cadena con los manejadores de edición.
Ajusta una curva a través posiciones designadas.
Ajusta una curva a través de posiciones en una superficie.
Dibuja una curva arrastrando el ratón.
Véase: Wikipedia: B-spline racionales no uniformes.
Las curvas de sección cónica se definieron en primer lugar como la intersección de: un cono circular recto de ángulo de vértice variable; un plano perpendicular a un elemento del cono. Según si el ángulo es inferior, igual o superior a 90 grados, se obtiene una elipse, una parábola o una hipérbola. Un arco es una parte de un círculo. Los comandos de Rhino permiten dibujar cónicos específicos y el comando general Cónico permite dibujar curvas cónicas de forma libre. Los cónicos son de grado 2.
Dibuja una curva de sección cónica con opciones de inicio, final, vértice y valor rho.
Dibuja un arco mediante las opciones de centro, inicio, ángulo y dirección.
Dibuja un círculo a partir del centro y el radio, el diámetro, puntos en la circunferencia y longitud de la circunferencia.
Dibuja una curva elíptica cerrada a partir de puntos focales, centro y bordes, rectángulo delimitador y alrededor de una curva.
Dibuja una curva hiperbólica desde puntos de foco, vértices o coeficiente.
Dibuja una curva parabólica desde el foco y el vértice o punto final.
Véase: Wikipedia: Cónico
Una espiral es una curva en un plano que gira alrededor de un punto central fijo a una distancia creciente o decreciente desde el punto.
Una hélice es una curva tridimensional que gira alrededor de un eje a una distancia constante o continuamente variable a la vez que se mueve paralelamente al eje.
Dibuja una curva helicoidal con opciones para número de giros, inclinación, vertical, invertir y alrededor una curva.
Dibuja una curva espiral con las opciones de número de giros, inclinación, plano, vertical y alrededor una curva.
Véase: Wikipedia: Espiral.
Crear curvas a partir de otros objetos
Rhino 6 for Mac © 2010-(Undefined variable: RhinoVariables.ThisYear) Robert McNeel & Associates. 04-jun.-2019