![]()
![]()
Editar
Hacer periódica
| Barra de herramientas | Menú |
|---|---|
|
|
Editar Hacer periódica |
El comando HacerPeriódica elimina puntos de torsión de una curva o superficie.
|
Curva periódica |
Una curva periódica es una curva suave cerrada. Las curvas periódicas permanecen suaves cuando se editan. |
|
Superficie periódica |
Las superficies periódicas son superficies cerradas (como una superficie cilíndrica) que se pueden deformar sin desarrollar puntos de torsión. Las superficies periódicas se crean automáticamente cuando las curvas de entrada son periódicas. |
| Opción en la línea de comandos | |
|---|---|
|
Suavizar |
Controla la eliminación de puntos de torsión. La opción Suavizar sólo está disponible cuando no hay objetos seleccionados. SíSuaviza los puntos de torsión de la curva y mueve los puntos de control para hacer una curva suave. NoLas posiciones de los puntos de control no cambian o cambian mínimamente (solo puede moverse un punto) y solo se modifica el vector nodal. 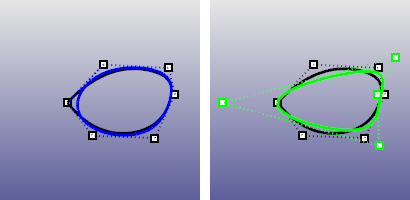
Suavizar=Sí (izquierda) y Suavizar=No (derecha). |
| Barra de herramientas | Menú |
|---|---|
|
|
|
El comando HacerNoPeriódica inserta un punto torsión en el inicio/final de una curva o superficie.
|
Curva no periódica |
Un curva no periódica es una curva cerrada con un punto de torsión en el inicio/final de la curva. Si se deforman curvas no periódicas cerca del inicio de la curva, pueden aparecer puntos de torsión. |
|
Superficie no periódica |
Una superficie no periódica es una superficie cerrada con un punto de torsión en el inicio/final de la superficie. Si se deforman superficies no periódicas cerca del inicio de la superficie, pueden aparecer puntos de torsión. Las superficies no periódicas se crean automáticamente cuando las curvas de entrada son no periódicas. Las superficies y las curvas no periódicas se deforman con esquinas puntiagudas en los puntos de torsión. |
Rhino 6 for Mac © 2010-(Undefined variable: RhinoVariables.ThisYear) Robert McNeel & Associates. 04-jun.-2019