Propiedades físicas de volumen de objetos abiertos/cerrados
Los objetos seleccionados como parte del comando Volumen deben delimitar un volumen. El modo más sencillo de asegurar esto es seleccionar objetos sólidos (cerrados, múltiples y orientados con la dirección normal apuntando hacia fuera). Sin embargo, se trata de casos donde es conveniente unir objetos para formar una polisuperficie o malla.
En estos casos, se pueden calcular las propiedades físicas de volumen de un grupo de objetos no sólidos.
Tiene que asegurarse de que:
![]() Los objetos encierran un volumen.
Los objetos encierran un volumen.
![]() Cada superficie se encuentra en el límite del volumen, no en su interior.
Cada superficie se encuentra en el límite del volumen, no en su interior.
![]() La normal de superficie o de malla apunta hacia fuera del volumen.
La normal de superficie o de malla apunta hacia fuera del volumen.
Pasos
![]() Utilice el comando Dir para comprobar o modificar la normal de superficie o de malla.
Utilice el comando Dir para comprobar o modificar la normal de superficie o de malla.
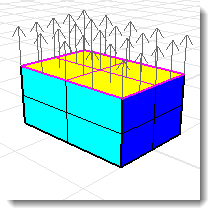
Seis superficies rectangulares o caras de malla con la orientación correcta definen el volumen de la caja.

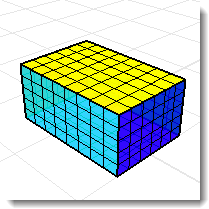
Sin la parte superior de la caja, los comandos de propiedades físicas de volumen darán un resultado sin significado.


Propiedades físicas de volumen de objetos no múltiples
Una polisuperficie o malla para la que cada borde es compartido al menos por dos caras se denomina múltiple. Los comandos de propiedades físicas de volumen dan por supuesto que cada cara delimita el volumen.
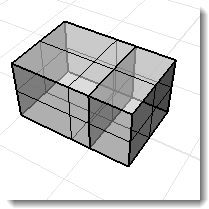
Polisuperficie no múltiple donde cada superficie no delimita un volumen. Los comandos de propiedades físicas de volumen darán un resultado sin significado.
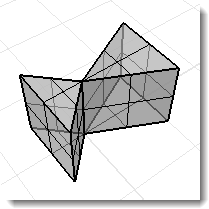
Polisuperficie no múltiple donde cada superficie delimita un volumen. Los comandos de propiedades físicas de volumen darán como resultado datos válidos.
Propiedades físicas de volumen de objetos no orientados
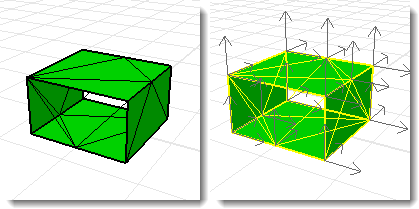
Es posible que una polisuperficie o una malla tengan orientaciones incoherentes en las caras.
Utilice el comando Dir para ver las normales de las caras. Un sólido correctamente orientado tendrá las normales apuntando hacia fuera.
Esta malla tiene normales incoherentes.
Para cambiar las normales en algunas caras de una polisuperficie
 Utilice los comandos Descomponer o ExtraerSup para aislar las caras con la dirección de la normal incorrecta.
Utilice los comandos Descomponer o ExtraerSup para aislar las caras con la dirección de la normal incorrecta.
 Utilice el comando Dir en las caras de manera individual para orientar correctamente las normales.
Utilice el comando Dir en las caras de manera individual para orientar correctamente las normales.
 Utilice el comando Unir para reconstruir la polisuperficie.
Utilice el comando Unir para reconstruir la polisuperficie.
Para cambiar las normales en mallas no orientadas
![]() Utilice el comando UnificarNormalesDeMalla.
Utilice el comando UnificarNormalesDeMalla.
Malla reparada con normales coherentes apuntando hacia fuera.
Información de cálculo de propiedades de masa
Los distintos campos de especialidad y libros de texto utilizan una nomenclatura y notación diferente, a veces contradictoria, para definir los momentos. El informe de los momentos de área o volumen se puede utilizar para calcular cualquiera de esos momentos. Para obtener el momento específico que necesite, tendrá que combinar distintos valores del informe de momentos.
Ejemplo
A modo de ejemplo, se muestra a continuación el informe de los momentos de área de un plano z constante con esquinas en 0,0,0 y 6,10,0.
Área = 60 (+/- 1e-008)
Centroide de área = 3,5,0 (+/- 1e-009,1e-009,0)
Momentos de área:
Momentos de primer orden
x: 180 (+/- 1e-007)
y: 300 (+/- 1e-007)
z: 0 (+/- 0)
Momentos de segundo orden
xx: 720 (+/- 1e-007)
yy: 2000 (+/- 1e-006)
zz: 0 (+/- 0)
Momentos de producto
xy: 900 (+/- 1e-007)
yz: 0 (+/- 0)
zx: 0 (+/- 0)
Momentos de inercia de área alrededor de los ejes de coordenadas universales
Ix: 2000 (+/- 1e-006)
Iy: 720 (+/- 1e-007)
Iz: 2720 (+/- 1e-006)
Radios de giro de área alrededor de los ejes de coordenadas universales
Rx: 5.77350269 (+/- 1e-009)
Ry: 3.46410162 (+/- 1e-009)
Rz: 6.73300329 (+/- 1e-009)
Momentos de inercia de área alrededor de los ejes de coordenadas del centroide
Ix: 500 (+/- 1e-007)
Iy: 180 (+/- 1e-007)
Iz: 680 (+/- 1e-007)
Radios de giro de área alrededor de los ejes de coordenadas del centroide
Rx: 2.88675135 (+/- 1e-009)
Ry: 1.73205081 (+/- 1e-009)
Rz: 3.36650165 (+/- 1e-009)
Los números entre paréntesis describen la precisión del cálculo.
A continuación se describen con precisión los valores del informe de momentos de área y volumen.
Momentos de primer orden
Los momentos de área de primer orden tienen unidades de longitud3. Los momentos de área de primer orden tienen unidades de longitud4. Cuando se trata el tema de momentos de área en el plano x-y, algunas disciplinas y libros de texto usan el símbolo Mx, para indicar el valor descrito como “Momentos de primer orden y”, mientras que otras disciplinas y libros de texto utilizan el mismo símbolo para indicar el valor descrito como "Momentos de segundo orden x:". Una situación similar ocurre con el símbolo My.
En términos de integrales, los momentos de área de primer orden se calculan de la siguiente manera:
Momento de área de primer orden x: valor = integral de x dA sobre el área,
Momento de área de primer orden y: valor = integral y dA sobre el área,
Momento de área de primer orden z: valor = integral z dA sobre el área.
De manera similar, los momentos de volumen de primer orden se calculan de la siguiente manera:
Momento de volumen de primer orden x: valor = integral de x dV sobre el volumen,
Momento de volumen de primer orden y: valor = integral de y dV sobre el volumen,
Momento de volumen de primer orden z: valor = integral de z dV sobre el volumen.
Para un área o un volumen, la relación entre los momentos de primer orden, el área o el volumen y el centroide de área es:
Coordenada x de centroide = (momento de primer orden x: valor)/M,
Coordenada y de centroide = (momento de primer orden y: valor)/M,
Coordenada y de centroide = (momento de primer orden z: valor)/M,
donde M es el área o volumen.
Momentos de segundo orden
Los momentos de área de segundo orden tienen unidades de longitud 4. Los momentos de volumen de segundo orden tienen unidades de longitud 5.
En términos de integrales, los momentos de área de segundo orden se calculan de la siguiente manera:
Momento de área de segundo orden xx: valor = integral de x2 dA sobre el área,
Momento de área de segundo orden yy: valor = integral de y2 dA sobre el área,
Momento de área de segundo orden zz: valor = integral de z2 dA sobre el área.
De manera similar, los momentos de volumen de segundo orden se calculan de la siguiente manera:
Momento de volumen de segundo orden xx: valor = integral de x2 dV sobre el volumen,
Momento de volumen de segundo orden yy: valor = integral de y2 dA sobre el volumen,
Momento de volumen de segundo orden zz: valor = integral de z2 dV sobre el volumen.
Momentos de producto
Los momentos de área de segundo orden tienen unidades de longitud 4. Los momentos de producto de volumen tienen unidades de longitud 5.
En términos de integrales, los momentos de producto de área se calculan de la siguiente manera:
Momento de producto de área xy: valor = integral de xy dA sobre el área,
Momento de producto de área yz: valor = integral de yz dA sobre el área,
Momento de producto de área zx: valor = integral zx dA sobre el área.
De manera similar, los momentos de producto de volumen se calculan de la siguiente manera:
Momento de producto de volumen xy: valor = integral de xy dV sobre el volumen,
Momento de producto de volumen yz: valor = integral de yz dV sobre el volumen,
Momento de producto de volumen zx: valor = integral de zx dV sobre el volumen.
Para un área o un volumen, los productos de inercia de sirven para calcular momentos de inercia en ejes que no son paralelos a un eje de coordenadas. En particular, un momento de inercia de área alrededor de cualquier eje se puede expresar como combinación lineal de área, momentos de área de primer orden, momentos de área de segundo orden y momentos de área de producto.
Momentos de inercia alrededor de los ejes de coordenadas universales
Los momentos de inercia de área tienen unidades de longitud 4. Los momentos de inercia de volumen tienen unidades de longitud 5. Los símbolos estándar Ix, Iy e Iz se usan para indicar los momentos de inercia de área alrededor de los ejes universales x, y, z, respectivamente.
En términos de integrales, los momentos de inercia de área alrededor de los ejes universales se definen de la siguiente manera:
Ix = integral de (y2 + z2) dA sobre el área,
Iy = integral de (z2 + x2) dA sobre el área,
Iz = integral de (x2 + y2) dA sobre el área.
Los momentos de inercia de volumen se definen de una manera similar.
Para un área o un volumen, los momentos de inercia alrededor de los ejes universales se calculan según los momentos de segundo orden de la siguiente manera:
Ix = momento de segundo orden yy: valor + momento de segundo orden zz: valor,
ly = momento de segundo orden zz: valor + momento de segundo orden xx: valor,
lz = momento de segundo orden xx: valor + momento de segundo orden yy: valor.
Radios de giro de alrededor de los ejes de coordenadas universales
Los radios de giro tienen unidades de longitud. Los libros de texto y de referencia de ingeniería utilizan con frecuencia los símbolos R o k para referirse a los radios de giro. El radio de giro de un área alrededor de un eje 3D se calcula con la raíz cuadrada de (momento de inercia de área alrededor del eje)/área.
De manera similar, el radio de giro de volumen se calcula con la raíz cuadrada de (momento de inercia de área alredor del eje)/área.
Para un área o un volumen, los radios de giro del área alrededor de los ejes del plano universal en el informe de momentos del área se calculan de la siguiente manera:
Rx = sqrt( Ix / M ),
Ry = sqrt( Iy / M ),
Rz = sqrt( Iz / M ),
donde M es el área o volumen.
Aquí, Ix, Iy y Iz son los momentos de inercia de área alrededor de los ejes del plano universal.
Momentos de inercia de alrededor de los ejes de coordenadas del centroide
Los radios de giro alrededor del centroide tienen unidades de longitud 4. Los momentos de inercia de volumen alrededor del centroide tienen unidades de longitud 5. Los símbolos estándar Ix, Iy e Iz se usan para indicar estos momentos de inercia del área.
En términos de integrales, los momentos de inercia de área alrededor del centroide de área del objeto se calculan de la siguiente manera:
Ix = integral de ((y-y0)2 +( z-z0)2) dA sobre el área,
Iy = integral de ((z-z0)2 +( x-x0)2) dA sobre el área,
Iz = integral de ((x-x0)2 + (y-y0)2) dA sobre el área,
Aquí, (x0>, y0, z0) es el centroide del área.
Los momentos de volumen de inercia sobre el centroide de volumen se definen de una manera similar.
Los momentos de inercia de área (o volumen) se expresan en términos de momentos de segundo orden, primer orden y volumen):
Ix = momento de segundo orden yy: valor
+ momento de segundo orden zz: valor
- 2*y0*(momento de primer orden y: valor)
- 2*z0*(momento de primer orden z: valor)
+ (y02+z02)*M,
ly = momento de segundo orden zz: valor
+ momento de segundo orden xx: valor
- 2*z0*(momento de primer orden z: valor)
- 2*x0*(momento de primer orden x: valor)
+ (z02+x02)*M,
lz = momento de segundo orden xx: valor
+ momento de segundo orden yy: valor
- 2*x0*(momento de primer orden x: valor)
- 2*y0*(momento de primer orden y: valor)
+ (x02+y02) *M,
donde M es el área o volumen.
Radios de giro de alrededor de los ejes de coordenadas del centroide
Los radios de giro alrededor del centroide tienen unidades de longitud. Para un área o volumen, los radios de giro alrededor del centroide del área en el informe de momentos se calculan de la siguiente manera:
Rx = sqrt( Ix / M ),
Ry = sqrt( Iy / M ),
Rz = sqrt( Iz / M ),
donde M es el área o volumen.
Aquí, Ix, Iy e Iz son los momentos de inercia de área (o volumen) alrededor del centroide del área o volumen.