Il comando Curvatura valuta la curvatura di una curva o superficie su un punto usando il raggio di un cerchio.
Passi
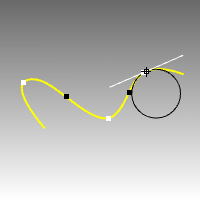
| 1. | Selezionare una curva. Il raggio di curvatura della curva in corrispondenza del puntatore viene indicato nella barra di stato e viene visualizzato un cerchio nero avente tale raggio, tangente alla curva nel punto in cui si trova il puntatore. Viene inoltre visualizzata una linea bianca tangente alla curva. I punti di colore bianco segnano i punti di massima curvatura in una porzione della curva in cui la curvatura inizia a decrescere in entrambe le direzioni dai punti. I punti di colore nero segnano i punti di minima curvatura in cui il cerchio di curvatura salta da un lato all'altro della curva. La curvatura sui punti di colore nero è sempre pari a 0. |
| 2. | Specificare un punto per segnare la curvatura con un cerchio, oppure premere Esc per terminare il comando. |
Per analizzare la curvatura di una superficie
| 1. | Selezionare una superficie. Man mano che si sposta il cursore, vengono visualizzati due semicerchi per mostrare la curvatura massima e minima nel punto corrispondente sulla curva. |
| 2. | Specificare un punto sulla superficie. |

Le seguenti informazioni di valutazione della superficie vengono visualizzate nell'area comandi:
| ● | Valutazione curvatura superficie al parametro (posizione) |
| ● | Punto 3D |
| ● | Normale 3D |
| ● | Curvatura principale massima e minima |
| ● | Curvatura gaussiana |
| ● | Curvatura media |
Nota
| ● | Ciascun punto su una curva "smooth" ha un cerchio che approssima la curva in quel punto. |
| ● | Il cursore esegue automaticamente degli snap ai punti di flesso della curva (i punti in cui cambia il segno della curvatura). |
| ● | Ciascun punto su una superficie "smooth" presenta due cerchi simili. Il cerchio con raggio maggiore è sempre ortogonale al cerchio con raggio minore. |
| ● | Le curvature principali sono l'inverso dei raggi degli archi. |
| ● | La curvatura Gaussiana è positiva quando entrambe le metà del cerchio puntano nella stessa direzione, negativa quando i cerchi puntano in direzioni opposte, e zero se una delle metà degenera in un linea. |
Opzione da linea di comando
SegnaCurvatura
Colloca un oggetto punto ed il cerchio di curvatura o i mezzi cerchi sul punto valutato sulla curva.
In questo modo, si ottiene un riscontro permanente quando il raggio di curvatura è infinito (la curvatura è zero, la curva è localmente piana, per esempio ai punti di flesso in cui la curvatura cambia da un lato all'altro) e non può essere valutato. Questo metodo non automatizza il rintracciamento dei punti di flesso, ma permette di marcarli manualmente.
Per capire la nozione di curvatura gaussiana di un punto su una superficie, occorre innanzitutto sapere cos'è la curvatura di una curva.
In qualsiasi punto di una curva sul piano, la linea che si avvicina di più alla curva che attraversa questo punto è la linea tangente. Possiamo anche trovare il cerchio che si avvicina di più, che attraversi questo punto e che sia tangente alla curva. Il reciproco del raggio di questo cerchio è la curvatura della curva in questo punto.
Il cerchio che si avvicina di più si può trovare sulla destra o sulla sinistra della curva. Considerando questo fatto, possiamo per esempio assegnare un segno positivo alla curvatura se il cerchio si trova sulla sinistra della curva ed attribuirle un segno negativo se il cerchio si trova sulla destra della curva. Si parla di curvatura con segno.
Una generalizzazione della curvatura applicata alle superfici è la curvatura della sezione normale. Dato un punto sulla superficie ed una direzione situata sul piano tangente della superficie in quel punto, la curvatura della sezione normale viene calcolata intersecando la superficie con il piano suddiviso dal punto, la normale alla superficie in quel punto e la direzione. La curvatura della sezione normale è la curvatura con segno di questa curva nel punto preso in considerazione.
Se guardiamo in tutte le direzioni sul piano tangente alla superficie nel punto analizzato e calcoliamo la curvatura della sezione normale in tutte le direzioni, otterremo un valore massimo ed un valore minimo.
Curvatura gaussiana
La curvatura gaussiana di una superficie in un punto è il prodotto delle curvature principali in quel punto. Il piano tangente di qualsiasi punto con una curvatura gaussiana positiva tocca la superficie in un solo punto, mentre il piano tangente di qualsiasi punto con una curvatura gaussiana negativa taglia la superficie. Qualsiasi punto con una curvatura media pari a zero ha una curvatura gaussiana negativa o pari a zero.
Curvature principali
Le curvature principali di una superficie in un punto rappresentano il minimo ed il massimo delle curvature normali in quel punto. (Le curvature normali sono le curvature delle curve sulla superficie situate su piani che includono il vettore tangente in un dato punto). Le curvature principali si usano per calcolare la curvatura gaussiana e media di una superficie.
Curvatura media
La curvatura media di una superficie in un punto è la metà della somma delle curvature principali in quel punto. Qualsiasi punto con una curvatura media pari a zero ha una curvatura gaussiana negativa o pari a zero.
Le superfici con una curvatura media ovunque pari a zero sono dette superfici minime. Le superfici con una curvatura media ovunque costante sono conosciute come superfici CMC (a curvatura media costante).
Le superfici CMC hanno la stessa curvatura media su tutta la superficie.
I processi fisici che si possono modellare con superfici CMC comprendono la formazione di bolle di sapone, sia libere che attaccate agli oggetti. Una bolla di sapone, diversamente da una semplice pellicola, racchiude un volume ed esiste in uno stato di equilibrio, dove la pressione leggermente maggiore all'interno della bolla viene equilibrata dalle forze della superficie minima della bolla stessa.
Le superfici minime sono il sottoinsieme delle superfici CMC, in cui la curvatura è ovunque zero.
I processi fisici che si possono modellare con superfici minime comprendono la formazione di pellicole di sapone che si estendono su oggetti fissi, come per esempio un cappio a filo metallico. Una pellicola di sapone non viene deformata dalla pressione dell'aria (che è uguale da entrambi i lati) ed è libera di minimizzare la propria area. Una bolla di sapone, invece, racchiude una quantità fissa di aria ed ha pressioni diverse al suo interno ed al suo esterno.
Vedi anche
Rhino for Mac © 2010-2015 Robert McNeel & Associates. 28-set-2015