Mit dem Befehl KrümmungsAnalyse kann die Krümmung einer Fläche mithilfe einer Falschfarbenanalyse untersucht werden.
Hinweis
| ● | Diese Werkzeuge können verwendet werden, um Informationen über Typ und Menge an Krümmung auf einer Fläche zu erhalten. Gaußsche und mittlere Krümmungsanalyse können aufzeigen, wenn und wo Anomalien (Besonderheiten) in der Krümmung einer Fläche vorhanden sind. |
| ● | Unannehmbare plötzliche Änderungen wie Bumps, Vertiefungen, flache Bereiche oder Wellen oder im Allgemeinen Krümmungsbereiche, die höher oder tiefer als die umgebende Fläche sind, können wenn nötig ermittelt und repariert werden. |
| ● | Gaußsche Krümmungsanzeige ist hilfreich bei der Entscheidung, ob eine Fläche in ein flaches Muster abgewickelt werden kann. |
| ● | Eine glatte Fläche besitzt zwei Hauptkrümmungen. Die Gaußsche Krümmung ist ein Produkt der Hauptkrümmungen. Die mittlere Krümmung ist der Durchschnitt der beiden Hauptkrümmungen. |
Vorgehen
| 1. | Wählen Sie Objekte aus. Die ausgewählte Fläche wird standardmäßig auf Gaußsche Krümmung untersucht. |
| 2. | Bestimmen Sie Stil und Intervall. |
Hinweis
| ● | Wenn Sie den Befehl Krümmungsanalyse verwenden und die ausgewählten Objekte kein Polygonnetz für die Flächenanalyse besitzen, wird ein unsichtbares Polygonnetz basierend auf Einstellungen im Dialogfenster Polygonnetzoptionen erzeugt. |
| ● | Die Polygonnetze für die Flächenanalyse sind in den Rhino-Dateien gespeichert. Diese Polygonnetze können groß sein. Der Befehl SchattierenAktualisieren und die Option Nur Geometrie speichern der Befehle Speichern und SpeichernUnter entfernen alle Flächenanalysenetze. |
| ● | Um eine NURBS -Freiformfläche richtig zu analysieren, benötigen die Analysebefehle normalerweise ein detailliertes Polygonnetz. |
Krümmung
Stil
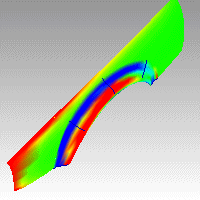
In den folgenden Abbildungen wird rot einem positiven Wert der Gaußschen Krümmung zugeteilt, grün einer Gaußschen Krümmung von null und blau einem negativen Wert der Gaußschen Krümmung.
Alle Punkte auf der Fläche mit Krümmungswerten zwischen den von Ihnen definierten Werten werden in der entsprechenden Farbe angezeigt. Punkte mit einem Krümmungswert, der sich zwischen den definierten Werten befindet, werden z. B. grün angezeigt. Punkte auf der Fläche mit Krümmungswerten, die sich außerhalb des roten Endes des Intervalls befinden, erscheinen rot und Punkte mit Krümmungswerten, die sich außerhalb des blauen Endes des Intervalls befinden, erscheinen blau.
Positive Krümmung
Ein positiver Gaußscher Krümmungswert bedeutet, dass die Fläche schüsselähnlich ist.

Negative Krümmung
Ein negativer Wert bedeutet, dass die Fläche Sattel-ähnlich ist.
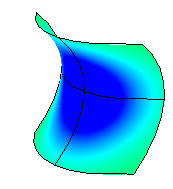
Null-Krümmung
Ein Wert von null bedeutet, dass die Fläche in mindestens eine Richtung flach ist. (Ebenen, Zylinder und Kegel besitzen eine Gaußsche Krümmung von null).

Wenn Sie wissen, welches Intervall des Krümmungswerts Sie analysieren möchten, geben Sie diese Werte in die Bearbeitungskästchen neben den roten und blauen Bereichen des "Regenbogens" ein. Die Werte, die Sie für rot verwenden, sollten nicht die gleichen sein, die Sie für blau verwenden; der Wert für rot kann aber größer oder kleiner als der Wert für blau sein.
Zeigt den absoluten Wert der mittleren Krümmung an. Es ist hilfreich, um Flächen mit abrupter Änderung in der Flächenkrümmung zu finden.
Wenn Sie eine Fläche im Abstand r versetzen oder eine Fläche mit einem Schnittball mit Radius r fräsen, wird jede Zone auf der Fläche, die sich mit einem Radius kleiner als r "krümmt" Probleme bereiten.
Im Falle eines Versatzes erhalten Sie ein verdrehtes Durcheinander, das durch sich selber verläuft. Im Falle einer Fräsung entfernt der Schnittball Material, das Sie behalten möchten.
In beiden Fällen sollten Sie die Frage beantworten können "Besitzt diese Fläche irgendeine Zone, die sich zu fest verbiegt?". Die Option Min. Radius sollte Ihnen helfen, diese Frage zu beantworten.
Definieren Sie ROT = r und BLAU = 1.5 x r
Sie können nicht beliebig auf der roten Fläche versetzen/fräsen. Blaue Zonen sollten sicher sein. Sie sollten jedoch Flächen von grün bis rot mit Vorsicht betrachten.
Diese Option ist hilfreich zur Erkennung von flachen Flecken. Geben Sie für blau einen relativ hohen Wert (10 >100 >1000) und für rot einen Wert nahe der Unendlichkeit ein. Rote Flächen im Modell markieren dann flache Flecken, wo die Krümmung praktisch null ist.
Intervall der Krümmung
Wenn Falschfarben-Mapping verwendet wird, analysiert der Befehl Krümmungsanalyse die Flächenkrümmung. Sie sollten Werte mit satten Computerfarben abbilden. Als Anfangspunkt verwenden Sie Automatisches Intervall und passen Sie die Werte an, damit sie symmetrisch aber mit den durch Automatisches Intervall ausgewählten Werten vergleichbar sind.
Der Befehl Krümmungsanalyse versucht, sich an die Einstellungen zu erinnern, die Sie bei der letzten Flächenanalyse verwendet haben. Wenn Sie die Geometrie einer Fläche stark verändert oder zu einer neuen Fläche gewechselt haben, sind diese Werte vielleicht nicht angebracht. In diesem Fall können Sie Automatisches Intervall verwenden, um automatisch einen Krümmungswert des Farb-Mappings zu berechnen, das zu einer guten Farbverteilung führt.
Wählen Sie diese Option aus, wenn Sie wollen, dass die maximale Krümmung an rot und die minimale Krümmung an blau gemappt wird. Auf Flächen mit extremer Krümmungsabweichung ist das Resultat ein eher uninformatives Bild.
 Isokurve anzeigen
Isokurve anzeigen
Zeigt Isokurven auf den Objekten an
Zur Aktivierung der Krümmungsanalyse für weitere Objekte.
Zur Deaktivierung der Krümmungsanalyse für ausgewählte Objekte.
Um die Gaußsche Krümmung eines Punktes auf einer Fläche verstehen zu können, müssen Sie zuerst wissen, was die Krümmung einer Kurve ist.
An jedem beliebigen Punkt auf einer Kurve in der Ebene ist die tangentiale Linie die Linie, die sich der Kurve durch diesen Punkt am meisten nähert. Wir können auch den Kreis finden, der sich am meisten nähert, durch diesen Punkt verläuft und tangential zur Kurve liegt. Der Kehrwert des Radius dieses Kreises ist die Krümmung der Kurve an diesem Punkt.
Der beste annähernde Kreis befindet sich wahrscheinlich entweder links der Kurve oder rechts davon. Wenn das wichtig ist, treffen wir eine Abmachung und geben z. B. der Krümmung ein Pluszeichen, wenn der Kreis links, und ein Minuszeichen, wenn der Kreis rechts von der Kurve liegt. Das wird Krümmung mit Zeichen genannt.
Eine Verallgemeinerung der Krümmung einer Fläche ist die Normalkrümmung. Bei einem Punkt auf der Fläche und einer Richtung auf der tangentialen Ebene der Fläche an diesem Punkt, wird die Krümmung normaler Schnittkurven berechnet, indem die Fläche mit der durch diesen Punkt definierten Ebene, der Flächennormalen an diesem Punkt und der Richtung geschnitten wird. Die Krümmung von normalen Schnittkurven ist die Krümmung mit Zeichen dieser Kurve am Punkt von Interesse.
Wenn wir alle Richtungen in der an der Fläche tangentialen Ebene an unserem Punkt betrachten und die Krümmung von normalen Schnittkurven in all diesen Richtungen berechnen, wird es einen maximalen und minimalen Wert geben.
Gaußsche Krümmung
Die Gaußsche Krümmung einer Fläche an einem Punkt ist das Produkt der Hauptkrümmungen an diesem Punkt. Die tangente Ebene eines beliebigen Punktes mit positiver Gaußschen Krümmung berührt die Fläche in einem einzelnen Punkt; die tangente Ebene eines beliebigen Punktes mit negativer Gaußschen Krümmung schneidet die Fläche. Alle Punkte mit einer mittleren Krümmung von null haben eine negative Gaußsche Krümmung oder eine von null.
Hauptkrümmungen
Die Hauptkrümmungen einer Fläche an einem Punkt sind die minimalen und maximalen Werte der normalen Krümmungen an diesem Punkt. (Die normalen Krümmungen sind die Krümmungen von Kurven auf der Fläche, die auf den Ebenen liegt, die den Vektor, der tangential zum gegebenen Punkt liegt, enthalten.) Hauptkrümmungen werden verwendet, um Gaußsche und mittlere Krümmungen der Fläche zu berechnen.
Mittlere Krümmung
Die mittlere Krümmung einer Fläche an einem Punkt ist halb so groß wie die Summe der Hauptkrümmungen an diesem Punkt. Alle Punkte mit einer mittleren Krümmung von null haben eine negative Gaußsche Krümmung oder eine von null.
Flächen mit einer mittleren Krümmung von null in allen Punkten sind minimale Flächen. Flächen mit konstanter mittlerer Krümmung werden oft CMC-Flächen (Constant Mean Curvature) genannt.
Flächen mit konstanter mittlerer Krümmung haben in allen Punkten auf der Fläche die gleiche mittlere Krümmung.
Flächen mit konstanter mittlerer Krümmung können zur Modellierung physikalischer Prozesse, wie die Erzeugung von Seifenblasen an Objekten angehängt oder frei, verwendet werden. Im Gegensatz zu einem einfachen Seifenfilm umschließt eine Seifenblase ein Volumen und existiert in einem Gleichgewicht, bei dem der leicht höhere Druck im Innern der Blase durch die Kräfte der minimalen Fläche der Blase ausgeglichen wird.
Minimale Flächen sind die Untermenge von Flächen mit konstanter mittlerer Krümmung, bei der die Krümmung in allen Punkten null ist.
Flächen mit konstanter mittlerer Krümmung können zur Modellierung physikalischer Prozesse, wie die Erzeugung von Seifenfilmen, die fixe Objekte spannt (z. B. Drahtschleifen), verwendet werden. Ein Seifenfilm wird nicht durch den Luftdruck (der auf beiden Seiten gleich ist) verzerrt und kann seine Fläche frei minimieren. Das steht im Gegensatz zur Seifenblase, die eine bestimmte Luftmenge einschließt und deren Druck innen und außen nicht gleich ist.
Mit dem Befehl KrümmungsanalyseAus wird das Dialogfenster Krümmung geschlossen und die Anzeige der Krümmungsanalyse geschlossen.
Siehe auch
Rhino for Mac © 2010-2015 Robert McNeel & Associates. 31. August 2015