![]()
분석
곡률 표시 원
| 도구모음 | 메뉴 |
|---|---|
|
|
분석 곡률 표시 원 |
Curvature 명령은 원의 반지름을 사용하여 커브 또는 서피스상의 한 점 위치에서 곡률을 계산합니다.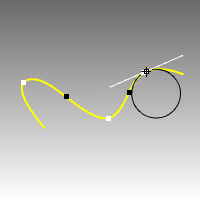
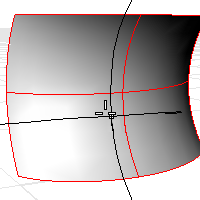
다음의 서피스 평가 정보가 명령 영역에 표시됩니다:
| 명령행 옵션 | |
|---|---|
|
곡률_표시 |
커브 상에서 계산되는 점에 점 개체와 곡률의 원 또는 반원을 배치합니다. 이것은 곡률의 반지름이 무한대로 계산할 수 없는 경우(커브의 팽창 방향이 바뀌는 변곡점 등에서, 곡률이 0 이고 커브는 일부분이 직선이 되어 있는), 항상 피드백으로 사용할 수 있습니다. 이것은 변곡점을 찾는 것을 자동화하지 않지만 수동으로 표시할 수 있게 합니다. |
| 도구모음 | 메뉴 |
|---|---|
|
|
분석 서피스 > 곡률 분석 |
CurvatureAnalysis 명령은 거짓 컬러(false color) 분석을 사용하여 시각적으로 서피스 곡률을 평가합니다. 거짓 컬러는 광선추적 모드를 제외한 모든 표시 모드에서 표시됩니다.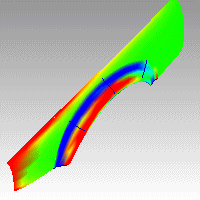
곡률 옵션
다음 이미지에서 빨간색은 양의 가우스 곡률값에 배정되었고, 녹색은 0의 가우스 배정에, 파랑은 음의 가우스 곡률값에 배정되었습니다.
곡률의 값이 사용자가 지정한 값 사이에 있는 서피스에 있는 점은, 그 값에 대응하는 색으로 표시됩니다. 예를 들어, 곡률의 값이 지정한 값의 중간 값을 가진 점은 녹색으로 표시됩니다. 빨간색의 범위 밖의 곡률의 값을 가진 서피스의 점은 빨간색으로 표시되어, 파란색의 범위 밖의 곡률의 값을 가진 서피스의 점은 파란색으로 표시됩니다.
가우스 곡률이 양의 값이면 서피스가 사발 모양임을 뜻합니다.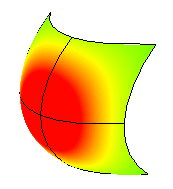
음의 값은 서피스가 안장 형태와 같음을 나타냅니다.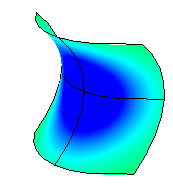
값이 0인 경우, 서피스는 적어도 한 방향에서 평평한 것을 의미합니다(평면, 원통, 원뿔의 가우스 곡률은 0입니다).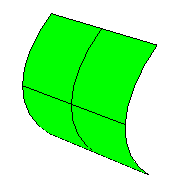
분석하고자 하는 곡률 값의 범위를 알고 있다면 "무지개"의 빨간색과 파란색 부분 옆의 편집 상자에 그 값을 입력합니다. 빨간색 값이 반드시 파란색 값과 달라야 합니다. 그러나 파란색 값보다 빨간색 값이 크거나 작아도 됩니다.
평균 곡률의 절대 값을 표시합니다. 서피스 곡률에서 급작스러운 변화가 있는 영역을 찾을 때 편리합니다.
거리r에서 서피스를 간격띄우기 하는 경우, 또는 반지름이 r인 절단공으로 서피스를 연마하는 경우, 서피스가 r보다 작은 반지름으로 "만곡시키는" 부분에는 문제가 발생합니다.
간격띄우기의 경우, 그 결과로 개체 자체가 비틀립니다. 연마의 경우에는 남겨두려는 재질을 절단공이 제거합니다.
서피스가 급격하게 구부려지는 부분이 있는지를 확인해야 하며 최소 반지름 옵션을 사용하면 도움이 됩니다.
빨간색 = r , 파란색 = 1.5 x r
서피스에서 빨간색은 간격띄우기 또는 연마가 불가능한 부분을 나타냅니다. 파란색은 가능한 부분입니다. 녹색에서 빨간색에 가까워지는 부분은 주의가 필요합니다.
이 옵션은 평평한 부분을 찾을 때 편리합니다. 파란색의 값을 비교적 높게 설정하고(10->100->1000) 빨간색의 값을 무한대에 가깝게 설정합니다. 모델의 빨간색 영역은 곡률의 값이 0에 가까운 평평한 부분을 나타냅니다.
거짓 컬러 매핑과 CurvatureAnalysis 명령을 사용하여 서피스의 곡률을 분석합니다. 컴퓨터의 채도에 값을 매핑 해야 합니다. 먼저 자동 범위를 클릭하고 자동 범위에서 선택된 것과 비슷한 크기의 값을 사용하여 값이 대칭이 되도록 조정합니다.
CurvatureAnalysis 명령은 마지막 서피스 분석을 실행했을 때의 설정을 사용하도록 시도합니다. 서피스의 지오메트리를 급격하게 변경한 경우 또는 새로운 서피스를 분석하려는 경우, 이 설정이 부적절할 수도 있습니다. 이러한 경우에 곡률과 색의 대응 매핑을 자동적으로 계산하는 자동 범위 옵션을 사용하여 곡률의 차이를 나타내는 색의 분포를 얻습니다.
최대 곡률을 빨간색으로, 최소 곡률을 파란색으로 매핑하려는 경우, 이 최대 범위의 옵션을 사용합니다. 그러나 극단적으로 곡률이 변화하는 서피스는 이 옵션의 이미지로 좋은 정보를 얻을 수 없는 경우가 있습니다.
 아이소커브 표시
아이소커브 표시서피스 아이소커브와 가장자리를 표시합니다.
분석 메쉬 밀도를 변경하기 위해 다각형 메쉬 옵션을 엽니다. 메쉬 밀도를 높이면 분석 정확도가 향상됩니다.
분석할 개체를 더 많이 선택합니다.
선택된 개체를 분석에서 제외시킵니다.
| 도구모음 | 메뉴 |
|---|---|
|
|
|
CurvatureAnalysisOff 명령은 곡률 대화상자를 닫고, 곡률 분석 표시를 끕니다.
| 도구모음 | 메뉴 | 앨리어스 |
|---|---|---|
|
|
분석 커브 > 곡률 그래프 켜기 |
COn |
CurvatureGraph 명령은 커브와 서피스 곡률을 그래프를 사용하여 시각적으로 평가합니다.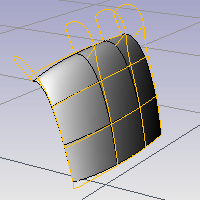
| 스팬 연속성 | |
|---|---|
|
접점 |
두 커브 스팬의 접선 방향은 동일하나, 곡률 그래프가 한 값에서 급격히 달라집니다(점프합니다). 차수 2의 커브 스팬은 G1으로, 접선 방향의 연속성이 일치하고 있을 뿐입니다. 곡률 연속성은 없습니다. 차수가 2인 커브에 3개의 스팬이 있습니다. 곡률 그래프가 스팬 간에 점프합니다.
|
|
곡률 연속성 |
곡률 그래프에서 값이 급격하게 변하는 곳은 없습니다. 첫 번째 스팬의 곡률 그래프의 끝이 두 번째 스팬의 곡률 그래프의 끝에 직접 연결되어 있습니다. 스팬이 접하는 곳에서 곡률의 값이 급격하게 변하지 않으므로, 이 곡률의 연속성은 G2이며, 곡률의 연속성이 있습니다. 그러나 첫 번째 스팬의 곡률 그래프의 변화의 정도는 두 번째 스팬의 곡률 변화의 정도와 다릅니다. 곡률의 값은 급격하게 변하지 않으나, 곡률의 변화율은 급격하게 변합니다. 차수가 3인 커브에 3개의 스팬이 있습니다. 곡률 그래프가 스팬 간에 끝과 끝이 이어집니다.
|
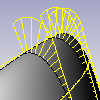
이 개념을 잘 이해하려면, Curvature 명령을 사용하여 커브를 따라 접촉하는 원의 움직임을 살펴 보세요.
곡률 그래프 옵션
변화의 크기는 실제보다 크게 표시될 수 있음을 기억하십시오. 곡률의 변화는 한 겹 칠한 페인트의 두께보다 두꺼워지지 않습니다. 표시 배율 설정에서 100은 1:1 곡률의 척도를 의미합니다.

그래프 세선의 수를 설정합니다.
 U
UU 방향에서만 서피스 세션을 표시합니다.
색 견본은 세선의 색을 설정합니다.
 V
VV 방향에서만 서피스 세션을 표시합니다.
색 견본은 세선의 색을 설정합니다.
추가로 선택된 개체의 곡률 그래프 분석을 켭니다.
선택된 개체의 곡률 그래프 분석을 끕니다.
| 도구모음 | 메뉴 | 앨리어스 |
|---|---|---|
|
|
분석 커브 > 곡률 그래프 끄기 |
COff |
CurvatureGraphOff 명령은 곡률 그래프 표시를 끕니다.
서피스에 있는 점의 가우스 곡률을 이해하려면, 먼저 커브의 곡률을 알아야 합니다.
평면에 있는 커브의 어느 점의 위치에서도, 이 점을 통과하는 커브의 근사값을 가장 잘 나타내는 선을 접선이라고 합니다. 또한 커브에 접하고 이 점을 통과하는 형상의 근사값을 가장 잘 나타내는 원을 구할 수 있습니다. 이 원의 반지름의 역수가 이 점에서의 커브의 곡률입니다.
커브의 근사값을 가장 잘 나타내는 원은 커브의 오른쪽 또는 왼쪽에 있을 수 있습니다. 이 구별이 중요한 경우, 관례적으로 원이 왼쪽에 있는 경우는 그 곡률을 양의 곡률로 보고, 오른쪽에 있는 경우에는 음의 곡률로 봅니다. 이를 부호가 붙은 곡률이라고 합니다.
곡률을 일반화하여 서피스에도 맞추는 개념으로 법곡률(Normal section curvature :법절단 곡률이라고도 함)이 있습니다.곡률을 일반화하여 서피스에도 맞추는 개념으로 이 있습니다. 서피스에 있는 점과, 그 점 위치에서 서피스 접평면의 방향을 선택합니다. 법곡률의 계산 방법은 그 점과, 그 점에서의 서피스 법선과 그 점에서의 선택된 방향선으로 정의된 평면을 서피스와 교차시킵니다. 그 결과로 나온 커브의 곡률을 계산합니다. 법곡률은 선택된 점에서의 부호가 붙은 곡률입니다.
점의 위치에서 서피스에의 접평면 위의 모든 방향을 봤을 때, 또한 이 모든 방향에서 법곡률을 계산했을 때는 최대값과 최소값이 있습니다.
한 점에서 서피스의 가우스 곡률은 그 점에서의 주 곡률의 곱입니다. 양의 가우스 곡률이 있는 점에서의 접평면은 서피스와 한 점에서만 접하지만, 음의 가우스 곡률이 있는 점에서의 접평면은 서피스를 분할합니다. 평균 곡률이 0인 점은 가우스 곡률의 값이 0이거나 음의 값입니다.
한 점에서 서피스의 주 곡률은 그 점에서 법곡률의 최소값과 최대값입니다(주어진 점에서 접벡터를 포함하는 평면에 있는 서피스의 커브의 법곡률). 주 곡률을 사용하여 서피스의 가우스 곡률과 평균 곡률을 계산합니다.
서피스에 있는 점에서 평균 곡률은 그 점에서의 주 곡률의 합의 1/2입니다. 평균 곡률이 0인 점은 가우스 곡률의 값이 0이거나 음이 값입니다.
모든 점에서 평균 곡률이 0인 서피스는 극소곡면이라고 합니다. 모든 점에서의 평균 곡률의 값이 일정한 서피스는 상수 평균 곡률 곡면(CMC -Constant Mean Curvature - Surface)이라고 불립니다.
상수 평균 곡률 곡면은 모든 점에서의 평균 곡률의 값이 일정합니다.
상수 평균 곡률 곡면은 모델링할 수 있는 물리적인 프로세스의 예로는 비눗방울(자유롭게 날고 있는 경우와 개체에 붙어 있는 경우)이 있습니다. 단순한 비누막과는 달리, 비눗방울은 체적을 가지며, 외부보다 다소 높은 비눗방울 내부의 압력과 비눗방울 자체의 표면적을 최소화하려는 힘이 균형을 이루고 있는 상태입니다.
극소곡면은 모든 점에서 곡률이 0인 상수 평균 곡률 곡면의 부분 집합입니다.
극소곡면으로 모델링할 수 있는 물리적 프로세스의 예로는 고정된 주형(철사 고리)에 매달린 비누막이 있습니다. 비누막은 기압에 의해 변형되지 않고(양쪽의 압력이 같으므로) 표면적을 가장 작게 하는 힘으로부터 자유롭습니다. 이것은 일정한 공기의 양을 가지고 있어 내부와 외부의 압력이 다른 비눗방울과 대조적입니다.
Rhino 6 for Mac © 2010-2020 Robert McNeel & Associates. 2020-12-08