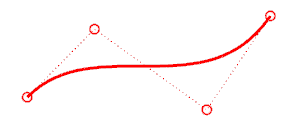
Join(結合)この章では、オブジェクトを分割したり、それらに穴を開けたり、再び結合するなどの編集機能を紹介します。これらのコマンドのいくつかは、曲線と曲線、サーフェスとサーフェス、またはサーフェスとポリサーフェスを接続したり、作成した曲線やポリサーフェスをそれらを構成するコンポーネントに分割します。
これらのコマンドにはJoin、Explode、Trim、Splitがあり、曲線とサーフェス、ポリサーフェスに使用できます。
Rebuild、ChangeDegree、Smoothコマンドは、曲線やサーフェスの基底の制御点構造を変更して曲線やサーフェスを変形します。
更に、オブジェクトには、それぞれに色やレイヤ、レンダリングマテリアル、その他の属性などのプロパティが割り当てられます。Propertiesコマンドは、これらのプロパティをコントロールします。
Join(結合)Joinコマンドは、曲線やサーフェスを接続し、1つのオブジェクトにします。例えば結合されたポリカーブは、直線のセグメント、円弧、ポリライン、自由曲線などでできています。Joinコマンドは隣接するサーフェスを接続し、ポリサーフェスを作成することもできます。
Explode(分解)Explodeコマンドは結合された曲線やサーフェス間の接続を解除します。ポリサーフェスを、制御点を使ってそれぞれのサーフェスを編集したい時などに便利な機能です。
Trim(トリム)と
Split(分割)TrimとSplitコマンドは似ています。違いは、オブジェクトをトリムすると、選択した部分が削除されるということです。オブジェクトを分割した場合は、両方の部分は削除されずに残ります。
Splitコマンドは、サーフェスを曲線、サーフェス、ポリサーフェス、またはそれ自体のアイソパラメトリック曲線で分割します。
Untrimコマンドは、サーフェスのトリム曲線を取り除きます。曲線を後で再利用するために保存しておくオプションがあります。
曲線やサーフェスの制御点を動かすことで、形を微調整できます。Rhinoには、制御点を編集するためのツールが多数用意されています。Rebuild、Fair、Smoothといったコマンドは、曲線やサーフェス上の制御点を自動的に配置し直す場合に使用できます。制御点をドラッグしたり少しずつ動かしたりするコマンドや、、HBarといったコマンドは、制御点を1つずつ、またはまとめて手作業で移動したい場合に使用します。
制御点の表示機能制御点を操作して曲線やサーフェスを編集するには、PointsOnコマンドを使って制御点を表示します。
制御点の編集を終了した後は、PointsOffコマンドを使うか、Escキーを押して、制御点を非表示にします。
ポリサーフェスの制御点は表示して編集することはできません。ポリサーフェスの制御点を編集すると、結合されたサーフェスのエッジをうっかり離してしまい、ポリサーフェスに「隙間」ができることがあるからです。
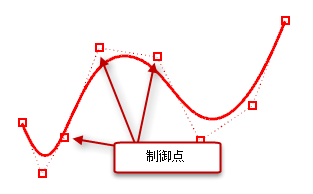
制御点を動かすと曲線またはサーフェスは形を変え、スムーズに再描画されます。曲線やサーフェスは制御点の位置を通るように再描画されるのではなく、制御点の新しい位置に引き付けられて再描画されます。そのため、オブジェクトを滑らかに変形することができます。制御点が表示されていると、Rhinoの変形コマンドを使ってそれらを操作することができます。また、サーフェスをリビルドして制御点を追加したり、再配置することもできます。
曲線に制御点を追加すると、曲線の形をより細密にコントロールできます。加えて、制御点を操作してキンクを取り除いたり、曲線を均一化したり、詳細を追加したり削除したりすることができます。Deleteキーは、曲線の制御点を削除します。制御点を削除すると曲線の形が変わります。
多項式は、y = 3x3のような関数です。多項式の「次数」は、関数の最も高い乗数です。例えば、3x3 –2x + 1の次数は3です。–x5 + x2の次数は5です。NURBS関数は、有理多項式で、NURBSの次数は多項式の次数です。NURBSモデリングの視点で見ると、(次数–1)は、それぞれのスパンで得られる最大の「湾曲」の数です。
例えば:
次数‑1の曲線には少なくとも2つの制御点がなければなりません。
線の次数は1より少ないです。線には0個の湾曲があります。
次数‑2の曲線には少なくとも3つの制御点がなければなりません。
放物線、双曲線、円弧、円(円錐断面曲線)の次数は2より小さいです。これらには1個の湾曲があります。
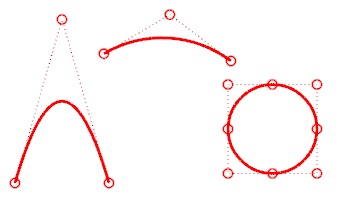
次数‑3の曲線には少なくとも4つの制御点がなければなりません。
3次ベジェの次数は3より少ないです。その制御点をジグザグ形状に配置すると、2つの湾曲が得られます。
