
六個矩形的曲面或網格可以形成一個包圍封閉空間的立方體。
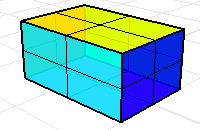
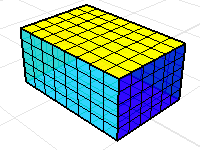
只要這個立方體少了一個面,體積質量內容指令計算出來的是沒有意義的結果。
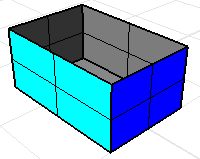

計算體積質量內容的指令選取的物件必需可以包圍一個封閉空間,要符合這個要求最簡單的方法是選取實體物件 (封閉、流形而且曲面的法線方向全部朝外) 做計算,但有些情形將物件組合成實體會造成某些不便。
遇到這種情形時,您可以選取一組非實體的物件來計算體積質量內容。
您必需確認:
| ● | 所有的物件可以包圍一個封閉的空間。 |
| ● | 每一個物件必需是封閉空間的外壁,不可以位於內部。 |
| ● | 所有曲面或網格的法線方向必需朝外。 |
步驟
| 4 | Use the Dir command to check or modify the surface or mesh normal.
六個矩形的曲面或網格可以形成一個包圍封閉空間的立方體。
只要這個立方體少了一個面,體積質量內容指令計算出來的是沒有意義的結果。
|
多重曲面或網格的每一個邊緣都被兩個面共用稱為流形,體積質量內容指令會認為這些面包圍著一個封閉空間。
所有曲面未能包圍封閉空間的非流形多重曲面計算出來的體積質量內容並沒有意義。
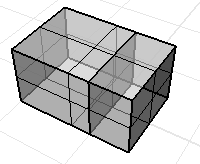
所有曲面可以包圍封閉空間的非流形多重曲面可以正確計算體積質量內容。
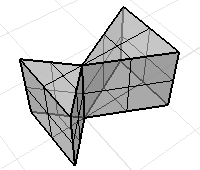
多重曲面或網格可能有法線方向不一致的情形。
Use the Dir command to display the face normals. A properly oriented solid will have outward pointing normals.
這個網格的法線方向不一致。
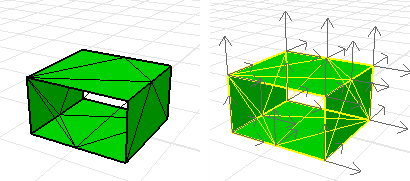
反轉多重曲面上某些曲面的法線方向。
| 1. | Use the Explode command or the ExtractSrf command to isolate the offending faces. |
| 2. | Use the Dir command on individual faces to properly orient the normals. |
| 3. | Use the Join command to reconstruct the polysurface. |
反轉法線方向不正確的網格
| 4 | Use the UnifyMeshNormals command. 修復後的網格的法線方向會朝著同一側。
|
不同的學科或教科書在定義不同的力矩時可能使用不同 ( 甚至會互相衝突 ) 的術語和符號。在面積或體積力矩報告中的資訊可以用來計算任何其它力矩,為了獲得您需要的力矩,您可能需要結合力矩報告中的幾個數值。
範例
對角位於 0,0,0 和 6,10,0 的矩形平面 (Z 座標固定),其面積力矩報告如下:
面積 = 60 (+/- 1e-08)
面積重心 = 3,5,0 (+/- 1e-09,1e-09,0)
面積力矩:
一次力矩
x: 180 (+/- 1e-007)
y: 300 (+/- 1e-007)
z: 0 (+/- 0)
二次力矩
xx: 720 (+/- 1e-007)
yy: 2000 (+/- 1e-006)
zz: 0 (+/- 0)
積力矩
xy: 900 (+/- 1e-007)
yz: 0 (+/- 0)
zx: 0 (+/- 0)
世界座標軸面積慣性力矩
Ix: 2000 (+/- 1e-006)
Iy: 720 (+/- 1e-007)
Iz: 2720 (+/- 1e-006)
世界座標軸面積迴轉半徑
Rx: 5.77350269 (+/- 1e-009)
Ry: 3.46410162 (+/- 1e-009)
Rz: 6.73300329 (+/- 1e-009)
重心座標軸面積慣性力矩
Ix: 500 (+/- 1e-007)
Iy: 180 (+/- 1e-007)
Iz: 680 (+/- 1e-007)
重心座標軸面積迴轉半徑
Rx: 2.88675135 (+/- 1e-009)
Ry: 1.73205081 (+/- 1e-009)
Rz: 3.36650165 (+/- 1e-009)
括弧中的數字表示計算的精確度。
面積和體積力矩報告中的數值的詳細敘述如下:
一次力矩
The area first moments have units of length3. The volume first moments have units of length4. When discussing area moments in the x-y plane, some disciplines and textbooks use the symbol Mx, to denote the value reported as "First Moments y:" while other disciplines and textbooks use the same symbol to denote the value reported as "First Moments x:". A similar confusing situation involves the symbol My.
以積分而言,面積一次力矩的定義如下:
面積一次力矩 x:值 = 面積積分 x dA,
面積一次力矩 y:值 = 面積積分 y dA,
面積一次力矩 z:值 = 面積積分 z dA。
類似地,體積一次力矩的定義如下:
體積一次力矩 x:值 = 體積積分 x dV,
體積一次力矩 y:值 = 體積積分 y dV,
體積一次力矩 z:值 = 體積積分 z dV。
對面積或體積而言,一次力矩與面積或體積及面積重心之間的關係是:
重心 x 座標 = ( 一次力矩 x:值 ) / M,
重心 y 座標 = ( 一次力矩 y:值 ) / M,
重心 z 座標 = ( 一次力矩 z:值 ) / M,
其中的 M 代表面積或體積。
二次力矩
面積二次力矩的單位是長度4,體積二次力矩的單位是長度5。
以積分而言,面積二次力矩的定義如下:
面積二次力矩 xx:值 = 面積積分 x2 dA,
面積二次力矩 yy:值 = 面積積分 y2 dA,
面積二次力矩 zz:值 = 面積積分 z2 dA,
類似地,體積二次力矩的定義如下:
Volume second moment xx: value = integral of x2 dV over the volume,
Volume second moment yy: value = integral of y2 dV over the volume,
Volume second moment zz: value = integral of z2 dV over the volume.
積力矩
面積的積力矩單位是長度4,體積的積力矩單位是長度5。
以積分而言,面積的積力矩定義如下:
面積的積力矩 xy:值 = 面積積分 xy dA,
面積的積力矩 yz:值 = 面積積分 yz dA,
面積的積力矩 zx:值 = 面積積分 zx dA,
體積的積力矩定義也很類似,如下:
體積的積力矩 xy:值 = 體積積分 xy dV,
體積的積力矩 yz:值 = 體積積分 yz dV,
體積的積力矩 zx:值 = 體積積分 zx dV。
以面積或體積而言,慣性積在計算不與任一座標軸平行的軸慣性力矩時很有用。尤其是任何軸面積慣性力矩可以由面積、面積一次力矩及面積二次力矩的線性組合表示。
重心座標軸慣性力矩
The area moments of inertia have units of length4. The volume moments of inertia have units of length5. It is fairly standard to use the symbols Ix, Iy, and Iz to denote the area moments of inertia about the world x-axis, y-axis, and z-axis, respectively.
以積分而言,世界座標軸的面積慣性力矩定義如下:
Ix= integral of (y2+ z2) dA over the area,
Iy= integral of (z2+ x2) dA over the area,
Iz= integral of (x2+ y2) dA over the area.
體積慣性力矩也是以類似的方式定義。
對於面積或體積而言,世界座標軸慣性力矩根據二次力矩定義:
Ix = 二次力矩 yy: 值 + 二次力矩 zz: 值,
Iy = 二次力矩 zz: 值 + 二次力矩 xx: 值,
Iz = 二次力矩 xx: 值 + 二次力矩 yy: 值。
世界座標軸的迴轉半徑
迴轉半徑的單位是長度,工程參考資料和教科書常以 R 或 k 表示迴轉半徑,3D 軸的面積回轉半徑定義為:(軸的面積慣性力矩) 的平方根 / 面積。
類似地,體積回轉半徑的定義為:(軸的體積慣性力矩) 的平方根 / 體積。
對於面積或體積而言,面積力矩報告中的世界座標軸迴轉半徑的計算方式如下:
Rx = 平方根 ( Ix / M ),
Ry = 平方根 ( Iy / M ),
Rz = 平方根 ( Iz / M ),
其中的 M 代表面積或體積。
Here the Ix, Iy, and Iz are the area moments of inertia about the world axes.
重心座標軸慣性力矩
重心的面積慣性力矩的單位是長度4,重心的體積慣性力矩的單位是長度5。一般標準是使用 Ix、Iy 及 Iz 代表面積慣性力矩。
以積分而言,物件面積重心的面積慣性力矩定義如下:
Ix = integral of ((y-y0)2 +( z-z0)2) dA over the area,
Iy = integral of ((z-z0)2 +( x-x0)2) dA over the area,
Iz = integral of ((x-x02 + (y-y0)2) dA over the area,
其中的 ( x0、y0、z0 ) 是面積重心。
體積重心的體積慣性力矩也是以類似的方式定義。
重心的面積 ( 或體積 ) 慣性力矩是以二次力矩、一次力矩及面積 ( 或體積 ) 表示:
Ix = 二次力矩 yy:值
+ 二次力矩 zz:值
- 2*y0*(first moment y: value)
- 2*z0*(first moment z: value)
+ (y02+z02)*M,
Iy = 二次力矩 zz:值
+ 二次力矩 xx:值
- 2*z0*(first moment z: value)
- 2*x0*(first moment x: value)
+ (z02+x02)*M,
Iz = 二次力矩 xx:值
+ 二次力矩 yy:值
- 2*x0*(first moment x: value)
- 2*y0*(first moment y: value)
+ (x02+y02) *M,
其中的 M 代表面積或體積。
重心座標軸的迴轉半徑
重心回轉半徑的單位是長度,就面積或體積而言,在力矩報告中的重心迴轉半徑的計算方式如下:
Rx = 平方根 ( Ix / M ),
Ry = 平方根 ( Iy / M ),
Rz = 平方根 ( Iz / M ),
其中的 M 代表面積或體積。
這裡的 Ix、Iy 及 Iz 是面積重心慣性力矩或體積重心慣性力矩。