GradÄndern

Ändert den Grad einer Kurve oder Fläche.

Schritte

Wählen Sie die Objekte aus.

Geben Sie einen Gradwert ein.

Für Flächen geben Sie Werte in die U- und V-Richtungen ein.

Option

Verformbar

Wenn Ja und der Grad der Kurve/Fläche nicht der gleiche ist wie der gewünschte, wird die neue Kurve/Fläche über einfache innere Knotenpunkte verfügen.

Wenn Nein und der Grad der Kurve/Fläche ist KLEINER als der gewünschte, wird die neue Kurve/Fläche die gleiche Geometrie und Parametrisierung haben wie das Original, aber Vielfaltsknoten haben = alte Vielfalt + neuer Grad - alter Grad.

Wenn der Grad der Kurve/Fläche GRÖßER als der gewünschte ist, wird die neue Kurve/Fläche eine Annäherung des Originals mit einfachen Knoten sein.

Bemerkungen

Der Befehl GradÄndern ändert den Grad des Polynoms, das zur Erzeugung der Kurve verwendet wird. Die Knotenstruktur der Kurven bleibt erhalten, allerdings werden zwischen den Knoten Kontrollpunkte eingefügt oder entfernt.

Oft ist es vorteilhafter, die Befehle KnotenEinsetzen und KnotenEntfernen zu verwenden, anstatt GradÄndern, weil Sie Kontrollpunkte mehr lokal hinzufügen/entfernen können.

Wenn die Fläche die gleiche Geometrie aber mehr Kontrollpunkte zum Bearbeiten haben soll, erhöhen Sie den Grad auf 5 mit der Option Verformbar auf Nein eingestellt. In diesem Fall können Sie den Befehl KnotenEinsetzen verwenden, der mehr Kontrollpunkte hinzufügt, ohne den Grad zu ändern.

Wenn Sie Ihre Geometrie in eine andere Anwendung exportieren, sollten Sie versuchen, den Grad Ihrer Flächen so tief wie möglich zu halten. Viele mechanische CAD-Systeme können keine Flächen importieren, die einen höheren Grad als 3 besitzen.

Die Anzahl Kontrollpunkte, die hinzugefügt oder entfernt wird, hängt vom Grad ab; je höher der Grad, umso größer die Kontrollpunktanzahl.

Wenn Sie den Grad einer Fläche erhöhen, ist diese nicht mehr periodisch. Verwenden Sie den Befehl PeriodischWandeln, um die Fläche wieder periodisch zu machen.

Objekte mit einem höheren Grad benötigen mehr Rechenleistung und Speicherplatz.

Grad

Ein Polynom ist eine Funktion wie y = 3x3 -2x +1.  Der "Grad" des Polynoms ist die größte Stärke der Variabel. Zum Beispiel ist der Grad von 3x3 -2x +1 gleich 3; der Grad von -x5 +x2 entspricht 5, usw. NURBS-Funktionen sind rationale Polynome und der Grad der NURBS ist der Grad des Polynoms. Vom Gesichtspunkt der NURBS-Modellierung ist (Grad –1) die maximale Anzahl "Biegungen", die Sie in jedem Segment erhalten.

Zum Beispiel:

Eine Linie verfügt über Grad 1. Sie hat null "Biegungen".

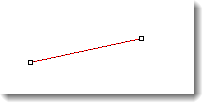
Grad 1: Linie.

Eine Parabel, Hyperbel, ein Bogen und Kreis (Kegelschnittkurven) haben Grad 2. Sie verfügen über eine Biegung.

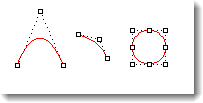
Grad 2: Parabel, Bogen, Kreis.

Eine kubische Bézier-Kurve hat Grad 3. Wenn Sie die Kontrollpunkte in einem Zick-Zack-Muster anordnen, können Sie zwei Biegungen erhalten.

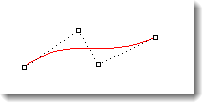
Kurve vom Grad 3.

Mehr unter