Descrizioni secondo la continuità
Una curva o una superficie si possono descrivere secondo la loro continuità Gn, dove n indica il valore crescente di "liscezza". Si considerino i segmenti su entrambi i lati di un punto su una curva:
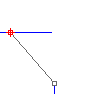
| ● | G0: Le curve si toccano in corrispondenza del punto di unione (posizione). |
| ● | G1: Le curve, in corrispondenza del punto di unione, hanno anche la stessa direzione tangente (tangenza). |
| ● | G2: Le curve, in corrispondenza del punto di unione, hanno anche lo stesso centro di curvatura (curvatura). |
Posizione (continuità G0) misura esclusivamente la posizione. Se gli estremi di ciascuna curva si trovano nello stesso punto dello spazio, le curve presentano continuità di posizione (G0) presso gli estremi. In altre parole, le due curve in questione si toccano in corrispondenza dei loro estremi.

Tangenza (continuità G1) misura la posizione e la direzione della curva agli estremi. In altre parole, le due curve non solo si toccano, ma vanno nella stessa direzione in corrispondenza del punto in cui si toccano.
La direzione è determinata dal primo e dal secondo punto su ciascuna curva. Se questi due punti ricadono su una linea, le due curve sono tangenti alle estremità.
La derivata prima delle due curve è la stessa nel punto in cui esse si toccano.
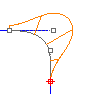
La continuità di curvatura (continuità G2) tra due curve misura la posizione, la direzione ed il raggio di curvatura alle estremità. Se il raggio di curvatura è lo stesso sull'estremità in comune, le curve avranno continuità di curvatura (G2). In altre parole, le curve non solo vanno nella stessa direzione nel punto in cui si incontrano, ma hanno anche lo stesso raggio in corrispondenza di tale punto. Questa condizione non è facile da determinare osservando semplicemente la disposizione dei punti.
Sia la derivata prima che la derivata seconda delle equazioni sono le stesse su quel punto.
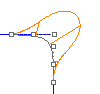
La continuità G3 aggiunge un terzo requisito: l'accelerazione planare. Le curve con continuità G3 si toccano, vanno nella stessa direzione, hanno lo stesso raggio e tale raggio ha lo stesso tasso di accelerazione in un determinato punto.
Le curve con continuità G3 hanno le stesse derivate terze.
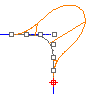
La continuità G4 è usata molto di rado, tuttavia può essere importante in alcuni casi. Le curve con continuità G4 soddisfano gli stessi requisiti delle curve G3, ma la loro accelerazione di curvatura è uguale nelle tre dimensioni.
Rhino for Mac © 2010-2015 Robert McNeel & Associates. 28-set-2015