階數

多項式是一個類似 (y= 3x3-2x+1) 的函數。多項式的次數是影響力最大的變數。例如 (3x3-2x+2) 的次數為 3；(-x5+x2) 的次數為 5，以此類推。 NURBS 函數是有理多項式，NURBS 的階數是多項式的次數。 從 NURBS 建模的角度來看，(階數 –1) 是曲線一個跨距中最大可以"彎曲"的次數。

例如：

直線的階數為 1，無法彎曲。

1 階：直線。

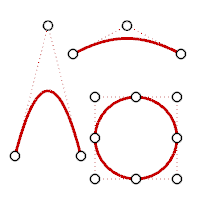
拋物線、雙曲線、圓弧、圓 (圓錐斷面曲線) 為 2 階曲線，可以彎曲一次。

2 階：雙曲線、圓弧、圓。

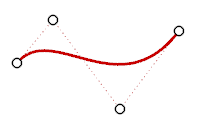
貝茲曲線屬於 3 階曲線，如果您將它的控制點排成 Z 形，曲線共彎曲了兩次。

3 階曲線。