![]()
曲面
展平曲面 >
攤平可展開的曲面
| 工具列 | 功能表 |
|---|---|
|
|
曲面 展平曲面 > 攤平可展開的曲面 |
UnrollSrf 指令可將 UV 兩個方向之中只有一個方向有曲率 (非直的) 的曲面或多重曲面攤開為平面。
| 指令行選項 | |
|---|---|
|
炸開 |
是不組合組展開的曲面。 否展開後的曲面以未展開前的共用邊緣組合在一起。 指定多重曲面展開後要分離的邊緣
|
|
標註 |
設定是否在展開前、後的曲面邊緣以對應編號的註解點標註。 |
|
保留內容 |
設定展開後的曲面是否套用物件原本的內容。 |
|
警告 |
當曲面攤平前後的面積差異百分比大於 公差值時彈出警告。 先執行指令再選取物件 (候選) 才會有這些選項。 面積差異公差設定曲面攤平前後要提出警告的面積差異百分比。 警告顯示設定警告訊息以指令行或對話框顯示。 指令行將警告訊息顯示在指令行,無需關閉警告訊息。 對話框將警告訊息以對話框顯示,警告訊息必需以按鈕關閉,可能干擾指令碼的運作。 |
Rhino 有一些指令可以建立或攤平可展開的曲面 (曲面上可以有洞或曲線)。
可展開的曲面就像是把無法延展、分離或收縮的材質捲起來一樣,例如:圓柱體、圓錐體及鋼板船殼。

想像一下使用鋁箔建立您想要的曲面形狀,如果在塑形的時候鋁箔皺了或是破了,您想要的曲面形狀即是不可展開的。球體就是一個不可展開的例子,鋁箔無法伏貼地包覆在球體上,現代汽車的車體外型及擋風玻璃都是屬於這一類的造型。
要以 UnrollSrf 指令攤平的曲面必需有一個方向是直的,在可展開的曲面上放一隻尺,當曲面的兩個邊緣之間尺可以完全接觸曲面時稱為尺規線。
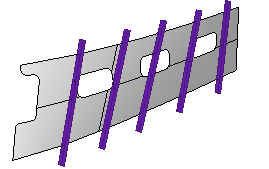
因為曲面有一個方向是直的,所以該曲面上的每一點的高斯曲率都是 0。Rhino 無法展開高斯曲率不是 0 或沒有任何一個方向是直的曲面。
因為可展開的曲面無法以任意兩條曲線建立,以 Loft 指令的可展開的型式建立的曲面型狀可能無法預期,形狀類似而且沒有銳角的曲線比較適合於建立可展開的曲面。
您可以使用高斯曲率分析找出曲面無法展開的部分。
可展開的曲面適用於設計機翼或水翼型式的曲面,但不適用於需要彎曲或展開金屬片的管路製作或布料剪裁。
建立可展開的曲面可能因為輸入曲線結構稍有不同或曲線的複雜呈度產生非常不一樣的結果。請儘量以結構簡單而且參數化完全相同的曲線做為輸入曲線才能產生較好的結果。
選取曲線時點選不同的端點可能產生不同的結果,有些時候您可以結合不同的結果產生較好的可展開的曲面。
可展開的曲面非必定是整平的曲面。
從 3D 曲面建立可展開的曲面,再將可展開的曲面展開,曲面展開後的面積與尺規線長度和原來的 3D 曲面之間會有誤差,但 Rhino 不會提出警告。
您可以展開無法展開的曲面。
Rhino 並沒有任何使曲面變得比較容易展開的方法,因為金屬具有某些程度的延展性 (尤其是鋁),即使和數學上可正確展開的曲面有相當程度的偏差,但仍然可以展開。
使用 CurvatureAnalysis 指令的高斯曲率分析協助建立曲面代替可展開的放樣是解決這個問題的一個方法,但除非曲面符合 UnrollSrf 指令的要求,否則 Rhino 無法以這個方式建立曲面。
許多設計師的設計需要重 3D 物件上的圖形展開為 2D 的平面圖形,3D 的曲面可以使用高斯曲率分析將曲面分為可以展開的與不可展開的兩種類型。
可展開的曲面可以毫無誤差的展開為平面,例如:圓錐體、平頂錐體、圓柱體。

球體或自由造型的曲面都是屬於無法精確展開的曲面。

雙向都有曲率的曲面展開時會有誤差,僅適用於有延展/收縮性的材質。
Curvature 指令可以顯示曲面的曲率圓。當您在曲面上移動滑鼠標記時,不可展開的曲面會顯示兩個圓弧。可展開的曲面會顯示一個圓弧與一條直線,代表曲面只有一個方向有曲率。
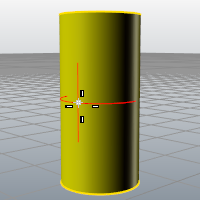

將不可展開的曲面展開成平面是一種複雜的運算,物件材質的延展性是重要因素之一。
可展開的曲面可以由平面的紙張經過裁切、摺疊完成,摺紙可以製作的物件就是可展開的物件。雖然紙張也可以組合成類似球體的形狀,但這樣的球體終究是非平滑的球體。如果您的物件必需使用有延展性的材質才能完成,那該物件是屬於 UnrollSrf 指令無法展開的物件。

Smash 指令可以用來展開雙向都有曲率的物件,但會有延展與收縮的誤差,適合用於展開具延展性的材質。
| 工具列 | 功能表 |
|---|---|
|
|
曲面 展平曲面 > 攤平曲面 UV |
UnrollSrfUV 的指令可展開曲面或多重曲面並維持輸入曲面的 UV 座標。
| 指令行選項 | |
|---|---|
|
炸開 |
是不組合組展開的曲面。 否展開後的曲面以未展開前的共用邊緣組合在一起。 指定多重曲面展開後要分離的邊緣
|
|
標註 |
設定是否在展開前、後的曲面邊緣以對應編號的註解點標註。 |
展平雙向都有曲率的曲面。
 Squish
Squish將展開時必定會有誤差 (兩個方向都有曲率) 的 3D 網格或 NURBS 曲面展開為平面。
Rhinoceros 7 © 2010-2022 Robert McNeel & Associates. 06-七月-2022