
曲面 >
展开曲面 >
压平双曲面
| 工具列 | 功能表 |
|---|---|
|
|
曲面 > 展开曲面 > 压平双曲面 |
Squish 指令将不可以展开的(UV 两个方向都是弯曲的)三维网格或 NURBS 曲面压平为到二维平面上。
Squish 指令会将压平的平面对应回原物件时收缩的区域以红色的点云标示,延展的区域以绿色的点云标示,并在收缩与延展最明显的位置以注解点标注变形量,最多可以标注十个边缘,注解点的数字是长度增加、减少的百分比。


展开前后的面积差异。
将二维图案变换到三维以后材质将被压缩。展开的平面对应回原来的物件时收缩的百分比为估算值。
将二维图案变换到三维以后材质将被延展。展开的平面对应回原来的物件时延展的百分比为估算值。
| 指令行选项 | |
|---|---|
|
分割接缝 |
展开封闭的曲面 (例如:圆柱曲面) 时从接缝切开。 |
|
维持边界 |
尽量维持边界的长度不变。 |
|
变形 |
设定收缩、延展的偏好,也可以自订变形的设定。 不设限不偏好收缩或延展。 延展为主当展开的平面对应回原来的 3D 物件时偏好延展。 只延展当展开的平面对应回原来的 3D 物件时偏好延展。 收缩为主当展开的平面对应回原来的 3D 物件时偏好收缩。 只收缩当展开的平面对应回原来的 3D 物件时只收缩不延展。 自定义A/自定义B/自定义C自定义变形设置。 有四个变形的参数可以设定。 边界延展边界收缩内部延展内部收缩这里的四个参数的设定预设都是 1,允许设为任何正数值。这四个参数是变形的偏好权重,例如您想尽量避免内部延展时可以像这样设定: 边界延展=1 边界收缩=1 内部延展=1 内部收缩=100 如果您想尽量维持边界的长度可以像这样设定: 边界延展=10 边界收缩=10 内部延展=1 内部收缩=1 自订设定用来设定 A、B、C 三组常用的设定。 |
|
材质 |
设定实际制造时使用的材质类型。 硬性当使用刚性材料制造时,从二维平面加工到三维曲面时应力最小。 软性当使用柔性材料制造时,尽可能的限制几何变形。 |
|
外侧 |
向上3D 曲面展开为 2D 平面时法线方向朝上。 向下3D 曲面展开为 2D 平面时法线方向朝下。 |
|
标示 |
在展开前后的物件上以红色与绿色的点云及注解点标注变形比例。 |
压平(Squish)是一个基于网格的算法,它将网格在空间网格和平面网格之间转换时,将通过一些限制尽可能的使网格面的面积和网格面边缘的长度变化最小。
例如,假设 A\B\C 是空间网格中一个三角网格面的三个顶点,a\b\c 是压平后平面网格中三角网格面上对应的三个顶点,那么边缘长度的计算如下:
d1 = |距离(A,B) - 距离(a,b)|
d2 = |距离(B,C) - 距离(b,c)|
d3 = |距离(C,A) - 距离(c,a)|
da = |面积(A,B,C) - 面积(a,b,c)|
DL = d1+d2+d3
DL2 = d12 + d22 + d32
DA = da
DA2 = da2
D = DL, DL2, DA 和 DA2 通过特点算法再结合起来
所谓“尽可能的使网格面的面积和网格面边缘的长度变化最小”就是在创建平面网格时,让这里的 D 的值最小。
在生产实践中,要计算有数千个细分面,也有很多计算 D 最小值的方法,但大多数能让 D 值最小的方法都没有实际意义,所以就要去约束压平得到的结果并约束空间点在平面上的具体位置,以防止平面网格自身发生折叠。
对于修剪的 NURBS 曲面,将在曲面排布一个密度网格,然后再将其压平。
压平的选项设置决定了 DA, DA2, D1 D2 是如何结合在一起的、允许通过更复杂的计算方式来计算 DA, DA2, D1, D2 的值、允许在拉伸或压缩的方向产生偏差。
但是,压平(Squish)算法还是太简单了,甚至无法模拟大多数材料的真实物理特性,尤其是那些在压缩或拉伸过程中厚度起重要作用的材料。
简而言之,如果材料昂贵、切割或弯曲费用高或是考虑其他时间成本和经济成本,可以尝试通过压平(Squish)获得一个初步的示意形态,但要得到在工厂中实际生产加工用的形态,还是需要通过材料学与制造相关的专业技术来解决。
| 工具列 | 功能表 |
|---|---|
|
|
|
SquishBack 指令将压平的平面上的曲线或点物件对应至原来的空间曲面。
假设要把 “Rhino” 的商标名称放到一个鞋的三维 NURBS 模型上。
先以 Squish 指令将鞋子的曲面与其上的曲线压平为平面。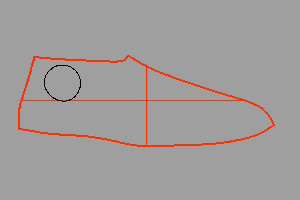
以 TextObject 指令在平面上的圆形曲线内建立“Rhino”的文字曲线。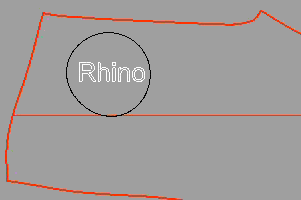
最后再使用 SquishBack 指令将文字曲线反向对应至鞋子的 3D 曲面上。
| 工具列 | 功能表 |
|---|---|
|
|
|
SquishInfo 指令显示展开的平面在展开时使用的设定。
旨在展开双向都有曲率的曲面。
将 UV 两个方向之中只有一个方向有曲率 (不是直的) 的曲面或多重曲面摊开为平面。
Rhinoceros 7 © 2010-2022 Robert McNeel & Associates. 29-4月-2022