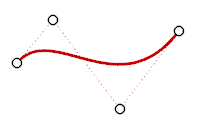
次数1: 線
多項式は、(y= 3x3-2x+1)のような関数です。多項式の「次数」は、変数の最も高い乗数です。例えば、(3x3-2x+2)の次数は3です。(-x5+x2)の次数は5です。NURBSNURBS関数は、有理多項式で、NURBSの次数は多項式の次数です。NURBSモデリングの視点で見ると、(次数–1)は、それぞれのスパンで得られる最大の「湾曲」の数です。
線は次数1です。線には0個の湾曲があります。

放物線、双曲線、円弧、円(円錐断面曲線)は次数2です。これらには1個の湾曲があります。
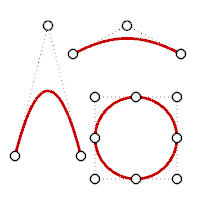
3次ベジェは次数3です。その制御点をジグザグ形状に配置すると、2つの湾曲が得られます。