Analyser les propriétés mécaniques d'un objet

Applications générales

CentroïdeAire

MomentsAire

CentroïdeVolume

MomentsVolume

Applications dans la construction navale

Hydrostatique

Informations sur les propriétés mécaniques de volume

Les objets sélectionnés dans la commande Volume doivent renfermer un volume. La meilleure façon d'en être sûr est de sélectionner des objets solides (variétés, fermées et orientées de sorte que la normale soit dirigée vers l'extérieur). Cependant, dans certains cas, la jonction des objets en une seule polysurface ou un seul maillage solide n'est pas très facile.

Les propriétés mécaniques du volume peuvent alors être calculées à partir d'un ensemble d'objets non solides.

Vous devez cependant vous assurer que :

• Les objets renferment un volume.
• Chaque surface est sur la limite du volume et non pas à l'intérieur.
• La normale de la surface ou du maillage est dirigée vers l'extérieur du volume.

Propriétés mécaniques du volume d'objets non-manifold

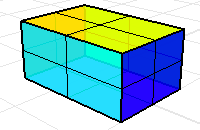
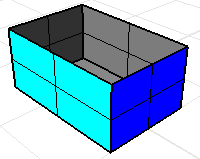
Une polysurface ou un maillage dont chaque bord est partagé par deux faces au maximum est appelé manifold. Les commandes de propriétés mécaniques du volume considèrent que chaque face limite le volume.

Une polysurface non manifold dont chaque surface ne limite pas un volume. Les commandes de propriétés mécaniques du volume donneront des résultats inutilisables.

Une polysurface dont chaque surface limite un volume. Les commandes de propriétés mécaniques du volume donneront des données valides.

Propriétés mécaniques du volume d'objets non orientés

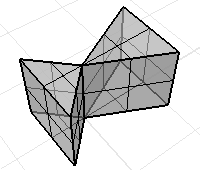
L'orientation des faces peut être incohérente sur une polysurface ou un maillage.

Utilisez la commande Direction pour afficher les normales des faces. Si un solide est correctement orienté, ses normales seront dirigées vers l'extérieur.

Les normales de ce maillage ne sont pas cohérentes.

Détails de calcul des propriétés mécaniques

Les différentes disciplines et livres utilisent des nomenclatures et notations différentes, voire contradictoires, quant à la définition des moments. Les informations données dans le rapport des moments de l'aire ou du volume peuvent être utilisées pour calculer tous ces types de moments. Afin d'obtenir le moment dont vous avez besoin, vous devrez peut-être combiner plusieurs valeurs du rapport des moments.

Exemple

Les moments de l'aire pour un plan de coordonnée z constante dont les sommets se trouvent à 0,0,0 et 6,10,0 sont indiqués ci-dessous :

Aire = 60 (+/- 1e-008)

Centroïde de l'aire = 3,5,0 (+/- 1e-009,1e-009,0)

Moments de l'aire :

Moments d'ordre
x: 180 (+/- 1e-007)
y: 300 (+/- 1e-007)
z: 0 (+/- 0)

Moments d'ordre
xx : 720 (+/- 1e-007)
yy : 2000 (+/- 1e-006)
zz : 0 (+/- 0)

Moments de produit
xy : 900 (+/- 1e-007)
yz : 0 (+/- 0)
zx : 0 (+/- 0)

Moments d'inertie par rapport aux axes du repère général
Ix : 2000 (+/- 1e-006)
Iy : 720 (+/- 1e-007)
Iz : 2720 (+/- 1e-006)

Rayons de giration par rapport aux axes du repère général
Rx : 5.77350269 (+/- 1e-009)
Ry : 3.46410162 (+/- 1e-009)
Rz : 6.73300329 (+/- 1e-009)

Moments d'inertie par rapport aux axes de coordonnées du centroïde
Ix : 500 (+/- 1e-007)
Iy : 180 (+/- 1e-007)
Iz : 680 (+/- 1e-007)

Rayons de giration par rapport aux axes de coordonnées du centroïde
Rx : 2.88675135 (+/- 1e-009)
Ry : 1.73205081 (+/- 1e-009)
Rz : 3.36650165 (+/- 1e-009)

Les chiffres entre parenthèses indiquent la précision du calcul.

Vous trouverez ci-après une description précise des valeurs données dans le rapport des moments d'aire et de volume.

Moments d'ordre 1

Les moments d'aire d'ordre 1 ont des unités de longueur3. Les moments de volume d'ordre 1 ont des unités de longueur4. Lors de l'explication des moments d'une aire dans le plan xy, certaines disciplines et certains livres utilisent le symbole Mx pour désigner la valeur donnée sous “Moments d'ordre 1 y:” alors que d'autres disciplines et d'autres livres utilisent le même symbole pour désigner la valeur donnée sous “Moments d'ordre 1 x:". Le symbole My pose aussi le même problème.

En termes d'intégrales, les moments d'ordre d'une aire sont définis par :

Moment d'aire d'ordre 1 x : valeur = intégrale de x dA sur l'aire.

Moment d'aire d'ordre 1 y : valeur = intégrale de y dA sur l'aire.

Moment d'air d'ordre 1 z : valeur = intégrale de z dA sur l'aire

De même, les moments de volume d'ordre 1 sont définis par :

Moment de volume d'ordre 1 : valeur = intégrale de x dV sur le volume.

Moment de volume d'ordre 1 y : valeur = intégrale de y dV sur le volume.

Moments de volume d'ordre 1 z : valeur = intégrale de z dV sur le volume.

Que ce soit pour l'aire ou le volume, la relation entre les moments d'ordre 1, l'aire ou le volume et le centroïde de l'aire est la suivante :

Coordonnée x du centroïde = (moment d'ordre 1 x: valeur)/M,

Coordonnée y du centroïde = (moment d'ordre 1 y: valeur)/M,

Coordonnée z du centroïde = (moment d'ordre 1 z: valeur)/M,

où M est l'aire ou le volume.

Moments d'ordre 2

Les moments d'aire d'ordre 2 ont des unités de longueur4. Les moments de volume d'ordre 2 ont des unités de longueur5.

En termes d'intégrales, les moments d'air d'ordre 2 sont définis par :

Moment d'aire d'ordre 2 xx : valeur = intégrale de x2 dAsur l'aire.

Moment d'aire d'ordre 2 yy: valeur = intégrale de y2 dA sur l'aire.

Moment d'aire d'ordre 2 zz : valeur = intégrale de z2 dA sur l'aire.

De même, les moments de volume d'ordre 2 sont définis par :

Moment de volume d'ordre 2 xx : valeur = intégrale de x2 dVsur le volume.

Moment de volume d'ordre 2 yy : valeur = intégrale de y2 dV sur le volume.

Moment de volume d'ordre 2 zz : valeur = intégrale de z2 dA sur le volume.

Moments de produit

Les moments d'aire de produit ont des unités de longueur4. Les moments de volume de produit ont des unités de longueur5.

En termes d'intégrales, les moments d'inertie d'une aire sont définis par :

Moment de produit xy : valeur = intégrale de xy dA sur l'aire.

Moment de produit d'aire yz: valeur = intégrale de yz dA sur l'aire.

Moment de produit d'aire zx: valeur = intégrale de zx dA sur l'aire.

De même, les moments de produit de volume sont définis par :

Moment de produit de volume xy : valeur = intégrale de xy dV sur le volume.

Moment de produit de volume yz : valeur = intégrale de yz dV sur le volume.

Moment de produit de volume zx : valeur = intégrale de zx dV sur le volume.

Que ce soit pour l'aire ou le volume, les produits d'inertie sont utiles pour le calcul des moments d'inertie par rapport à des axes qui ne sont pas parallèles aux axes des coordonnées. En d'autres termes, un moment d'inertie d'une aire par rapport à un axe peut être exprimé sous forme de combinaison linéaire d'une aire, de ses moments d'ordre 1, de ses moments d'ordre 2 et de ses moments de produit.

Moments d'inertie par rapport aux axes du repère général

Les moments d'inertie d'une aire ont des unités de longueur4. Les moments d'inertie d'un volume ont des unités de longueur5. On utilise normalement les symboles Ix, Iy et Iz pour désigner les moments d'inertie d'une aire par rapport aux axes du repère général x, y et z respectivement.

En termes d'intégrales, les moments d'inertie d'une aire par rapport aux axes du repère général sont définis par :

Ix = intégrale de (y2 + z2) dA sur l'aire.

Iy = intégrale de (z2 + x2) dA sur l'aire.

Iz = intégrale de (x2 + y2) dA sur l'aire.

Les moments d'inertie d'un volume sont définis d'une manière semblable.

Que ce soit pour l'aire ou le volume, en termes de moments d'ordre 2, les moments d'inertie par rapport aux axes du repère général sont définis par :

Ix = moment d'ordre 2 yy: valeur + moment d'ordre 2 zz: valeur,

Iy = moment d'ordre 2 zz: valeur + moment d'ordre 2 xx: valeur,

Iz = moment d'ordre 2 xx: valeur + moment d'ordre 2 yy: valeur.

Rayons de giration par rapport aux axes du repère général

Les rayons de giration ont des unités de longueur. Les références en ingénierie et les livres utilisent souvent R ou k pour désigner les rayons de giration. Le rayon de giration de l'aire par rapport à un axe 3D est défini comme la racine carrée de (moment d'inertie de l'aire par rapport à l'axe)/aire.

De même, le rayon de giration du volume est défini par la racine carrée de (moment d'inertie du volume par rapport à l'axe)/volume.

Que ce soit pour l'aire ou le volume, les rayons de giration par rapport aux axes du repère général dans le rapport des moments de l'aire sont calculés comme suit :

Rx = racine carrée( Ix / M ),

Ry = Racine carrée( Iy / M ),

Rz = Racine carrée( Iz / M ),

où M est l'aire ou le volume.

Dans ce cas Ix, Iy et Iz sont les moments d'inertie de l'aire par rapport aux axes du repère général.

Moments d'inertie par rapport aux axes de coordonnées du centroïde

Les moments d'inertie d'une aire par rapport au centroïde ont des unités de longueur4. Les moments d'inertie d'un volume par rapport au centroïde ont des unités de longueur5. On utilise normalement les symboles Ix, Iy et Iz pour désigner ces moments d'inertie de l'aire.

En termes d'intégrales, les moments d'inertie d'une aire par rapport au centroïde de l'aire de l'objet sont définis par :

Ix = intégrale de ((y-y0)2 +( z-z0)2) dA sur l'aire,

Iy = intégrale de ((z-z0)2 +( x-x0)2) dA sur l'aire,

Iz = intégrale de ((x-x0)2 + ( y-y0)2) dA sur l'aire,

Ici (x0>, y0, z0) est le centroïde de l'aire.

Les moments d'inertie d'un volume par rapport au centroïde du volume sont définis d'une manière semblable :

Les moments d'inertie d'une aire (ou d'un volume) sont exprimés en termes de moments d'ordre 2, de moments d'ordre 1 et de volume :

Ix = moment d'ordre 2 yy: valeur 

Iy = moment d'ordre 2 zz: valeur 

Iz = moment d'ordre 2 xx: valeur 

où M est l'aire ou le volume.

Rayons de giration par rapport aux axes de coordonnées du centroïde

Les rayons de giration par rapport au centroïde ont des unités de longueur. Que ce soit pour l'aire ou le volume, les rayons de giration par rapport au centroïde dans le rapport des moments sont calculés comme suit :

Rx = racine carrée(Ix / M ),

Ry = racine carrée( Iy / M ),

Rz = racine carrée( Iz / M ),

où M est l'aire ou le volume.

Dans ce cas Ix, Iy et Iz sont les moments d'inertie de l'aire (ou du volume) par rapport au centroïde de l'aire ou du volume.