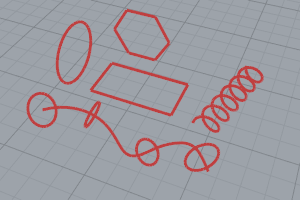
Dessiner des lignes et des courbes | Modélisation 3D avec Rhino

Une courbe dans Rhino est similaire à un morceau de fil de fer. Elle peut être droite ou ondulée, ouverte ou fermée.

Une polycourbe est une courbe composée de plusieurs segments joints par leurs extrémités.

Rhino vous offre de nombreux outils pour dessiner des courbes. Vous pouvez dessiner des lignes droites, des polylignes formées par des segments de lignes connectés, des arcs, des cercles, des polygones, des ellipses, des hélices et des spirales.

Vous pouvez aussi dessiner des courbes en utilisant des points de contrôle et dessiner des courbes qui passent par des points sélectionnés.

Lignes et polylignes

Une ligne est une courbe de degré 1 sans courbure. Une polyligne est un ensemble de segments de ligne ou d'arc joints ensemble.

Ligne

Dessiner un segment de ligne simple.

LigneParPoints

Ajuster une ligne sur des points, des points de contrôle et des nuages de points.

Polyligne

Dessiner une polyligne composée de plusieurs segments avec des options définissant l'utilisation de segments d'arc ou de ligne, la fermeture et les aides de ligne de repérage.

Polygone

Dessiner un polygone avec un certain nombre de côtés avec les options inscrit/circonscrit, à partir du bord, en forme d'étoile, autour d'une courbe et vertical.

Rectangle

Dessiner une polyligne rectangulaire fermée avec des options définissant le point de départ au centre, l'utilisation de trois points, l'orientation et l'arrondi des sommets avec des arcs ou des coniques.

Courbes de forme libre

Les courbes de forme libre dans Rhino sont des courbes NURBS. Une courbe NURBS est définie par son ordre, un ensemble de points de contrôle avec différents poids et un vecteur de nœud.

Chaînette

Crée une courbe représentant une chaîne ou un câble suspendu par ses extrémités.

Courbe

Dessiner une courbe à partir des positions des points de contrôle .

CourbePoignée

Dessiner des courbes de Bézier en chaîne en utilisant les poignées d'édition.

CourbeInterp

Ajuster une courbe passant par les points sélectionnés.

CourbeInterpSurSurf

Ajuster une courbe passant par des points sur une surface.

Esquisser

Faire glisser la souris pour dessiner une courbe.

Courbes de section coniques

Les courbes de section coniques ont d'abord été définies comme l'intersection entre : un cône de révolution dont l'angle au sommet varie et un plan perpendiculaire à un élément du cône. En fonction de l'angle, aigu, droit, ou obtus on obtient une ellipse, une parabole ou une hyperbole. Un arc est une partie de cercle. Rhino possède des commandes permettant de dessiner des coniques spécifiques ainsi que la commande Conique qui permet de dessiner des courbes coniques de forme libre. Les coniques sont des courbes de degré 2.

Conique

Dessiner une courbe de section conique avec des options définissant le point de départ, la fin, le sommet et la valeur Rho.

Arc

Dessiner un arc en définissant les options de centre, point de départ, angle et direction.

Cercle

Dessiner un cercle à partir de son centre et de son rayon, du diamètre, de points sur sa circonférence et de la longueur de sa circonférence.

Ellipse

Dessiner une courbe elliptique fermée à partir des foyers, du centre et des bords, du rectangle de contour et autour d'une courbe.

Hyperbole

Dessiner une courbe hyperbolique à partir de ses foyers, ses sommets ou un coefficient.

Parabole

Dessiner une courbe parabolique à partir de son foyer et de son sommet ou d'une extrémité.

Hélice et spirale

Une spirale est une courbe sur un plan qui s'enroule autour d'un centre fixe à une distance de celui-ci augmentant ou diminuant de façon continue.

Une hélice est une courbe en trois dimensions qui tourne autour d'un axe à une distance constante, ou variant de façon régulière, tout en se déplaçant parallèlement à l'axe.

Hélice

Dessiner une courbe en forme d'hélice avec des options définissant le nombre de tours, l'espacement, l'orientation ou le dessin autour d'une courbe.

Spirale

Dessiner une courbe en forme de spirale avec des options définissant le nombre de tours, l'espacement, l'orientation ou le dessin autour d'une courbe.

Voir aussi