![]()
Analyse
Cercle de courbure
| Barre d'outils | Menu |
|---|---|
|
|
Analyse Cercle de courbure |
La commande Courbure évalue la courbure d'une courbe ou d'une surface en un point en utilisant le rayon d'un cercle.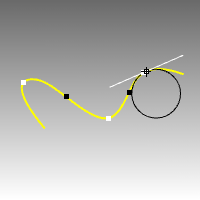
Les informations suivantes sont affichées dans la ligne de commandes :
| Options de la ligne de commande | |
|---|---|
|
MarquerCourbure |
Place un objet ponctuel et dessine le cercle ou les demi-cercles de courbure au niveau du point analysé sur la courbe. Ceci permet d'avoir des indications permanentes lorsque le rayon de courbure est infini (courbure égale à zéro, la courbe est plane localement, par exemple aux points d'inflexion lorsque le bombement de la courbe change d'un côté à l'autre) et ne peut donc pas être analysé. Cette technique ne permet pas de trouver automatiquement les points d'inflexion mais elle vous permet de les marquer manuellement. |
|
Tapez SousCourbe pour sélectionner une partie d'une courbe. |
|
| Barre d'outils | Menu |
|---|---|
|
|
Analyse Surface > Analyser la courbure |
La commande AnalyseCourbure analyse la courbure de la surface en utilisant des fausses couleurs. Les fausses couleurs sont affichées dans toutes les modes d'affichage sauf le mode Lancer de rayons.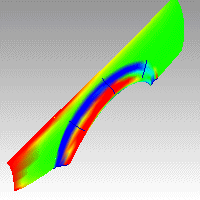
Options de la courbure
Dans l'image ci-dessous, le rouge est assigné aux valeurs positives de la courbure gaussienne, le vert aux courbures gaussiennes nulles et le bleu aux valeurs négatives de la courbure gaussienne.
Les points de la surface dont la valeur de la courbure est comprise entre les valeurs spécifiées seront affichés avec la couleur correspondant à cette plage de valeur. Par exemple, les points dont la valeur de courbure se trouve à mi-distance entre les valeurs spécifiées seront affichés en vert. Les points de la surface dont la valeur de courbure est au-delà de l'extrémité rouge de l'intervalle seront affichés en rouge et les points dont la valeur de courbure est au-delà de l'extrémité bleue de l'intervalle seront affichés en bleu.
Une courbure Gaussienne positive signifie que la surface est en forme de bol.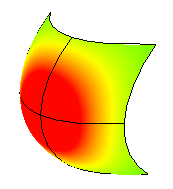
Une valeur négative signifie que la surface est en forme de selle.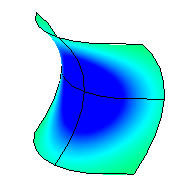
Une valeur nulle signifie que la surface est plane dans au moins une direction. (Les plans, les cylindres et les cônes ont une courbure gaussienne nulle).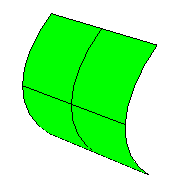
Si vous connaissez l'intervalle de valeurs de courbure que vous voulez analyser, entrez ces valeurs dans les cases se trouvant à côté des portions bleu et rouge du nuancier. Les valeurs que vous entrez pour le rouge doivent être différentes des valeurs données pour le bleu mais elles peuvent être plus grandes ou plus petites que pour le bleu.
Affiche la valeur absolue de la courbure moyenne. Cette option est utile pour trouver des zones où la courbure de la surface change brusquement.
Si vous voulez décaler une surface sur une distance r ou si vous voulez usiner une surface avec une bille de coupe de rayon r, toute partie de la surface dont le rayon de gauchissement est plus petit que r causera problème.
Dans le cas d'un décalage, vous obtiendrez une cassure se repliant sur elle-même. Dans le cas d'un usinage, la bille de découpe enlèvera des parties que vous voulez garder.
Dans ces cas, vous devez pouvoir répondre à la question : « Cette surface présente-t-elle une zone trop courbée ? » L'option Rayon minimum devrait vous aider à répondre à cette question.
Valeurs dans la boîte de dialogue : ROUGE = r et BLEU = 1.5 x r
Vous ne pouvez pas appliquer de décalage ni d'usinage sur les parties rouges de la surface. Les zones bleues sont correctes. Vous devrez traiter avec précaution les zones entre le vert et le rouge.
Cette option est utile pour la détection d'un point plat. Définissez la valeur du bleu assez haute (10 > 100 > 1000) et la valeur du rouge proche de l'infini. Les zones rouges indiqueront alors des points plats où la courbure est pratiquement nulle.
La commande AnalyseCourbure analyse la courbure de surfaces à l'aide d'une plaquage de fausses couleurs. Vous devez plaquer des valeurs correspondant aux couleurs informatiques saturées. Comme point de départ, utilisez Intervalle automatique et ajustez ensuite les valeurs pour qu'elles soient symétriques et toujours proches de celles sélectionnées par Intervalle automatique.
La commande AnalyseCourbure essaie de reprendre les paramètres que vous avez utilisés la dernière fois que vous avez analysé une surface. Si vous avez changé la géométrie de la surface ou si vous avez changé de surface, ces valeurs ne seront peut-être pas appropriées. Dans ce cas vous pouvez utiliser Intervalle automatique pour calculer automatiquement la valeur de courbure du plaquage qui donnera une bonne distribution de couleur.
Choisissez cette option si vous voulez que la courbure maximum soit indiquée en rouge et la courbure minimum en bleu. Sur des surfaces présentant un très grand écart de courbure, cette option peut donner une image ne fournissant presque aucune information intéressante.
 Afficher les bords et isoparamétriques
Afficher les bords et isoparamétriquesAffiche les bords ou courbes isoparamétriques sur les objets analysés.
Ouvre les Options de maillage pour modifier la densité du maillage d'analyse. Si la densité du maillage est augmentée, la précision d'analyse est améliorée.
Permet de sélectionner d'autres objets à analyser.
Supprime les objets sélectionnés de l'analyse.
| Barre d'outils | Menu |
|---|---|
|
|
|
La commande AnalyseCourbureDésactivée ferme la boîte de dialogue d'analyse de la courbure et désactive l'affichage de l'analyse de courbure.
| Barre d'outils | Menu | Alias |
|---|---|---|
|
|
Analyse Courbe > Activer le diagramme de courbure |
COn |
La commande DiagrammeCourbure analyse la courbure de la courbe ou de la surface en utilisant un diagramme.
| Continuité au niveau des intervalles | |
|---|---|
|
Tangent |
Même si les intervalles de la courbe sont tangents les uns par rapport aux autres, le diagramme de courbure passe subitement (saute) d'une valeur à une autre. Les intervalles d'une courbe de degré 2 sont de type G1 ou uniquement tangents. Il n'y a pas de continuité de courbure. Une courbe de degré 2 avec trois intervalles. Le diagramme de courbure saute entre les intervalles.
|
|
Continuité de courbure |
Le diagramme de courbure ne présente pas de sauts. Le diagramme de courbure du premier intervalle rejoint bout-à-bout le diagramme de courbure du deuxième intervalle. Cette courbe présente une continuité de courbure (G2) entre ses intervalles car sa courbure ne passe pas subitement d'une valeur à une autre. Cependant, l'aspect du diagramme de courbure du premier intervalle n'est pas le même que celui du deuxième intervalle. Ainsi, même si la courbure reste la même, le taux de courbure change brusquement. Une courbe de degré 3 avec trois intervalles. Le diagramme de courbure est connecté bout à bout entre les intervalles.
|
Pour mieux comprendre ce concept, essayez la commande Courbure et observez le cercle osculateur lorsqu'il se déplace le long des courbes.
Options du diagramme de courbure
Définit la taille des indicateurs de courbure. N'oubliez pas que l'échelle des changements peut être exagérée. Les changements sur la courbure ne devraient pas être plus épais qu'une feuille de papier. Une échelle d'affichage de 100 est équivalente à une échelle de courbure de 1:1.

Définit le nombre d'indicateurs de courbure.

 U
UAffiche les indicateurs des surfaces dans la direction u uniquement.
La palette de couleurs définit la couleur des indicateurs.
 V
VAffiche les indicateurs des surfaces dans la direction v uniquement.
La palette de couleurs définit la couleur des indicateurs.
Active l'affichage du diagramme de courbure pour d'autres objets sélectionnés.
Désactive l'affichage du diagramme de courbure sur les objets sélectionnés.
| Barre d'outils | Menu | Alias |
|---|---|---|
|
|
Analyse Courbe > Désactiver le diagramme de courbure |
COff |
La commande DiagrammeCourbureDésactivé désactive l'affichage du diagramme de courbure.
Pour comprendre la courbure gaussienne d'un point sur une surface vous devez tout d'abord savoir ce qu'est la courbure d'une courbe.
En tout point d'une courbe dans un plan, la ligne se rapprochant le plus de la courbe qui passe par ce point est la ligne tangente. Nous pouvons aussi rechercher le cercle passant par ce point, se rapprochant le plus de la courbe et tangent à celle-ci. L'inverse du rayon de ce cercle est la courbure de la courbe en ce point.
Le cercle se rapprochant le plus de la courbe peut se trouver à gauche ou à droite de celle-ci. Compte tenu de ce fait, nous pouvons alors convenir de donner le signe positif à une courbure si le cercle se trouve à gauche et négatif si le cercle se trouve à droite de la courbe
La courbure de section normale est une des généralisations de la courbure appliquée aux surfaces. Soit un point sur une surface et une direction reposant sur le plan tangent à la surface en ce point, la courbure de section normale est calculée en prenant l'intersection de la surface avec le plan défini par ce point, la normale de la surface en ce point et la direction. La courbure de section normale est la courbure positive ou négative de cette courbe au point en question.
Si nous regardons dans toutes les directions dans le plan tangent à la surface au point en question et si nous calculons la courbure de section normale dans toutes ces directions, nous obtiendrons une valeur maximale et une valeur minimale.
La courbure gaussienne d'une surface en un point est le produit des courbures principales en ce point. Le plan tangent de tout point dont la courbure gaussienne est positive touche la surface en un seul point, alors que le plan tangent de tout point dont la courbure gaussienne est négative coupe la surface. Tout point dont la courbure moyenne est nulle présente une courbure gaussienne négative ou nulle.
Les courbures principales d'une surface en un point sont les valeurs minimale et maximale des courbures normales en ce point. (Les courbures normales sont les courbures des courbes sur la surface reposant sur les plans contenant le vecteur tangent au point en question). Les courbures principales sont utilisées pour calculer les courbures gaussienne et moyenne de la surface.
La courbure moyenne d'une surface en un point est la moitié de la somme des courbures principales en ce point. Tout point dont la courbure moyenne est nulle présente une courbure gaussienne négative ou nulle.
Les surfaces dont la courbure moyenne est nulle en tout point sont des surfaces minimales. Les surfaces dont la courbure moyenne est constante en tout point sont souvent appelées surfaces à courbure moyenne constante (CMC).
Les surfaces CMC ont la même courbure moyenne en tout point.
Les surfaces CMC peuvent être utilisées pour modéliser des procédés physiques tels que la formation de bulles liées à des objets ou libres. Une bulle, à la différence d'un simple film, contient un volume et existe dans un équilibre où une pression un peu supérieure à l'intérieure de la bulle est compensée par les forces de surface minimale de la bulle elle-même.
Les surfaces minimales forment le sous-ensemble des surfaces CMC dont la courbure est nulle en tout point.
Les surfaces minimales peuvent être utilisées pour modéliser des procédés physiques tels que la formation de films liés à des objets fixes comme des cercles de fils de fer. Un film n'est pas déformé par la pression de l'air (qui est égale des deux côtés) et il est possible de minimiser son aire. Ce qui n'est pas le cas pour la bulle, qui renferme une quantité fixe d'air et dont les pressions sont différentes à l'intérieur et à l'extérieur.
Rhinoceros 7 © 2010-2021 Robert McNeel & Associates. 13-juil.-2021