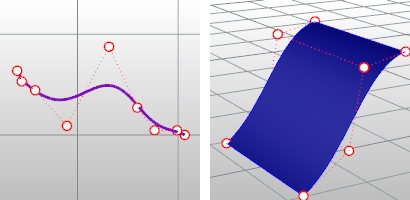
曲线控制点(左)与曲面控制点(右)。
控制点决定了一条曲线的形状,曲线上每个点的位置是通过若干个控制点加权得到的。每个点的加权根据控制参数而变化,对于一个阶数为 d 的曲线,权重值在参数空间 d+1 的范围内都不为零,权重根据度数d的多项式函数(基函数)而改变,在区间的边界处,基函数平滑地变为零,平滑程度由多项式的次数决定。
控制点越多就越能逼近一条给定的曲线,但只有一类曲线可以用限定数量的控制点精确表示,这就是 NURBS 曲线。 NURBS 曲线的每个控制点都具有标量权重,因此可以在不提升控制点数量的情况下控制曲线的形状,特别是它可以用一组二次曲线精确表示圆和椭圆这样的曲线,NURBS中的“有理”一词指的就是这些权重。
三维控制点在三维建模中被大量使用,三维控制点就是平时用来代表三维空间上具体位置的“点”。
