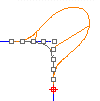
一个曲线或曲面可以被描述为具有 Gn 连续性,n 是表示光滑度的增量,即在曲线上取一点,然后分析该点与其两侧线段的关系。
请参考: 维基百科: Geometric continuity
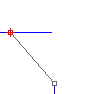
只测量两条曲线端点的位置是否相同,两条曲线的端点位于同一个位置时称为位置连续 (G0),换句话说就是两条曲线的端点相接。 
测量两条曲线端点的位置及方向是否相同,换句话说就是两条曲线的端点相接且方向一致。
曲线端点的方向是由第一、二个控制点决定,两条曲线相接点的前两个控制点 (共四个控制点) 位于同一直线上时称为正切。
两条曲线在相接点的一阶导数相同。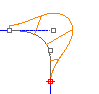
测量两条曲线端点的位置、方向及曲率是否相同,三者都相同时称为曲率连续 (G2),换句话说就是两条曲线的端点不只相接,连方向与半径都一样。曲率连续无法以控制点的位置来判断。
两条曲线在相接点的一阶、二阶导数相同。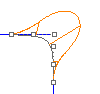
G3 连续比 G2 增加一个条件,两条曲线的端点除了位置、方向及半径一致以外,半径的变化率也必需相同。
G3 连续的曲线在相接点的一阶、二阶、三阶导数皆相同。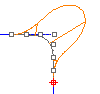
G4 连续极少用到,但可能在某些特殊案例很重要。G4 连续需要 G3 连续的所有条件以外,在 3D 空间的曲率变化率也必需相同。