オブジェクトのマスプロパティを解析する

一般

AreaCentroid

AreaMoments

VolumeCentroid

VolumeMoments

マリーンデザイン

AttachGHSData

Hydrostatics

体積マスプロパティについて

体積コマンドの一部として選択されたオブジェクトは体積を包括している必要があります。これを確実にする一番簡単な方法は、ソリッドオブジェクト（閉じた、多様の、外に法線が向いているオブジェクト）を選択することです。しかし、時によってオブジェクトをこのようなポリサーフェスやメッシュに結合するのは不便な場合もあります。

このような場合、マスプロパティはソリッドでないオブジェクトの集まりから計算することができます。

下の条件が必要です。

• オブジェクトの集まりが体積を包括している。
• それぞれのサーフェスが、体積の内側でなく境界にある。
• サーフェスまたがメッシュの法線が体積から外を向いている。

非多様体オブジェクトの体積マスプロパティ

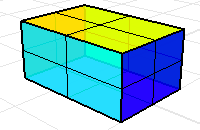
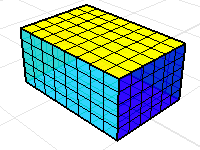
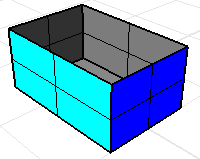
最大2面ですべてのエッジが共有されているポリサーフェスまたはメッシュを、多様体と呼びます。体積マスプロパティコマンドは、すべての面は体積を包括する境界であると想定します。

それぞれのサーフェスが体積を囲んでいない非多様体ポリサーフェスの例です。体積マスプロパティコマンドは意味のない結果を返します。

それぞれのサーフェスが体積を囲んでいる非多様体ポリサーフェスの例です。体積マスプロパティコマンドは有効な結果を返します。

向きの揃っていないオブジェクトの体積マスプロパティ

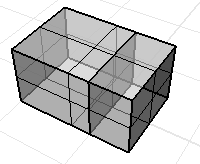
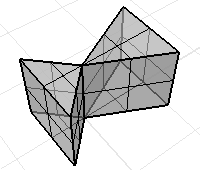
ポリサーフェスまたはメッシで、面の向きが揃っていない可能性がある場合があります。

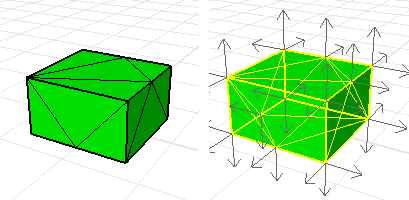
面の法線を表示するには、Dirコマンドを使用します向きが正しいソリッドの法線は外を向いています。

このメッシュの法線は揃っていません。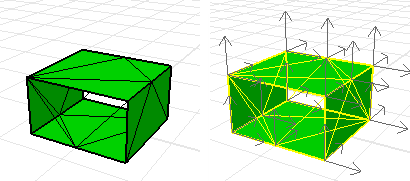

マスプロパティ計算の詳細

分野や教科書によっては、それぞれのモーメントの定義に使う用語法と表記法が異なったり、相矛盾したりするものまであります。面積または体積モーメントレポートの情報からどのモーメントでも計算できます。しかし、必要なモーメントを得るためにモーメントレポートのいくつかの値を合わせて計算しなければならない場合もあります。

例

頂点が0,0,0と6,10,0にあって、 z座標が一定である平面の面積モーメントのレポートを下に示します。

面積 = 60 (+/- 1e-008)

面積重心 = 3,5,0 (+/- 1e-009,1e-009,0)

面積モーメント:

一次モーメント
x: 180 (+/- 1e-007)
y: 300 (+/- 1e-007)
z: 0 (+/- 0)

二次モーメント
xx: 720 (+/- 1e-007)
yy: 2000 (+/- 1e-006)
zz: 0 (+/- 0)

積モーメント
xy: 900 (+/- 1e-007)
yz: 0 (+/- 0)
zx: 0 (+/- 0)

ワールド座標軸での慣性面積モーメント
Ix: 2000 (+/- 1e-006)
Iy: 720 (+/- 1e-007)
Iz: 2720 (+/- 1e-006)

ワールド座標軸での面積旋回半径
Rx: 5.77350269 (+/- 1e-009)
Ry: 3.46410162 (+/- 1e-009)
Rz: 6.73300329 (+/- 1e-009)

重心座標軸での慣性面積モーメント
Ix: 500 (+/- 1e-007)
Iy: 180 (+/- 1e-007)
Iz: 680 (+/- 1e-007)

重心座標軸での面積旋回半径
Rx: 2.88675135 (+/- 1e-009)
Ry: 1.73205081 (+/- 1e-009)
Rz: 3.36650165 (+/- 1e-009)

括弧の中の数字は計算の精度を示します。

面積および体積モーメントレポートの値の正確な定義を下に示します。

一次モーメント

面積の一次モーメントの単位は長さ3（3乗）です。体積の一次モーメントの単位は長さ4（4乗）です。X-Y平面にある面積の一次モーメントを取り上げる場合、xを「一次モーメント y:」の値とする分野や教科書もありますが、反対にこの記号を「一モーメント x:」の値とする分野や教科書もあります。Myという記号についても同様です。

積分による面積の一次モーメントの定義は次の通りです。

面積の一次モーメント x: 値 = x dAの面積積分

面積の一次モーメント y: 値 = y dAの面積積分

面積の一次モーメント z: 値 = z dAの面積積分

体積の一次モーメントも次のように定義されます。

体積の一次モーメント x: 値 = x dVの体積積分

体積の一次モーメント y: 値 = y dVの体積積分

体積の一次モーメント z: 値 = z dVの体積積分

面積（体積）の一次モーメントと面積（体積）と面積重心の関係は次の通りです。

重心 x 座標 = (一次モーメント x: 値)/M

重心 y 座標 = (一次モーメント y: 値)/M

重心 z 座標 = (一次モーメント z: 値)/M

Mは面積または体積です。

二次モーメント

面積の二次モーメントの単位は長さ4（4乗）です。体積の二次モーメントの単位は長さ5（5乗）です。

積分による面積の二次モーメントの定義は次の通りです。

面積の二次モーメント xx: 値 = x2 dAの面積積分

面積の二次モーメント yy: 値 = y2 dAの面積積分

面積の二次モーメント zz: 値 = z2 dAの面積積分

体積の二次モーメントも次のように定義されます。

体積の二次モーメント xx: 値 = x2 dVの体積積分

体積の二次モーメント yy: 値 = y2 dVの体積積分

体積の二次モーメント zz: 値 = z2 dVの体積積分

積モーメント

面積の積モーメントの単位は長さ4（4乗）です。体積の積モーメントの単位は長さ5（5乗）です。

積分による面積の積モーメントの定義は次の通りです。

面積の積モーメント xy: 値 = xy dAの面積積分

面積の積モーメント yz: 値 = yz dAの面積積分

面積の積モーメント zx: 値 = zx dAの面積積分

体積の積モーメントも次のように定義されます。

体積の積モーメント xy: 値 = xy dVの体積積分

体積の積モーメント yz: 値 = yz dVの体積積分

体積の積モーメント zx: 値 = zx dVの体積積分

面積および体積の慣性乗積は座標軸に平行しない軸中心の慣性モーメントの計算に使用できます。より詳しくいえば、任意の軸中心の慣性面積モーメントは面積、面積の一次モーメント、面積の二次モーメント、そして面積の積モーメントの一次結合で求められます。

ワールド座標軸中心の慣性モーメント

面積の慣性モーメントの単位は長さ4（4乗）です。体積の慣性モーメントの単位は長さ5（5乗）です。Ix、Iy、Izの記号を使用して、ワールド座標のx軸、y軸、z軸中心の慣性面積モーメントを表すのが標準的になっています。

積分によるワールド座標軸中心の慣性面積モーメントの定義は次の通りです。

Ix= (y2+ z2) dAの面積積分

Iy= (z2+ x2) dAの面積積分

Iz= (x2+ y2) dAの面積積分

慣性体積モーメントは同じような形で定義されます。

面積および体積の二次モーメントによるワールド座標軸中心の慣性面積モーメントの定義は次の通りです。

Ix = 二次モーメント yy: 値 + 二次モーメント zz: 値

Iy = 二次モーメント zz: 値 + 二次モーメント xx: 値

Iz = 二次モーメント xx: 値 + 二次モーメント yy: 値

ワールド座標軸中心の面積旋回半径

面積旋回半径の単位は長さの単位です。工学の参考書や教科書はよく旋回半径をRまたはkの記号で表します。3D軸中心の面積旋回半径は（（軸中心の慣性面積モーメント / 面積）の平方根）と定義されます。

同様に体積旋回半径は（（軸中心の慣性体積モーメント / 体積）の平方根）と定義されます。

面積および体積モーメントのレポートにあるワールド座標軸中心の面積旋回半径の計算方法は次の通りです。

Rx = ( Ix / M )の平方根

Ry = ( Iy / M )の平方根

Rz = ( Iz / M )の平方根

Mは面積または体積です。

ここのIx、Iy、Izは、ワールド座標軸中心の慣性面積モーメントです。

重心座標軸中心の慣性モーメント

重心座標軸中心の慣性面積モーメントの単位は長さ4（4乗）です。重心座標軸中心の慣性体積モーメントの単位は長さの5（5乗）です。Ix、Iy、 Izの記号を使用してこの慣性面積モーメントを表すのも標準的になっています。

積分によるオブジェクトの重心座標軸中心の慣性面積モーメントの定義は次の通りです。

Ix = ((y-y0)2 +( z-z0)2) dAの面積積分

Iy = ((z-z0)2 +( x-x0)2) dAの面積積分

Iz = ((x-x0)2 + (y-y0)2) dAの面積積分

ここの(x0>, y0, z0)とは面積の重心を示します。

重心座標軸中心の慣性体積モーメントは同じような形で定義されます。

慣性面積（または体積）モーメントは次のように、二次モーメント、一次モーメント、そして面積（または体積）で定義されます。

Ix = 二次モーメント yy: 値

Iy = 二次モーメント zz: 値

Iz = 二次モーメント xx: 値

Mは面積または体積です。

重心座標軸中心の旋回半径

重心座標軸中心の旋回半径の単位は長さの単位です。面積および体積モーメントのレポートにある重心座標軸中心の旋回半径の計算方法は次の通りです。

Rx = ( Ix / M )の平方根

Ry = ( Iy / M )の平方根

Rz = ( Iz / M )の平方根

Mは面積または体積です。

ここのIx, Iy, and Izは、面積（または体積）重心座標軸中心の慣性面積または体積モーメントです。