![]()
Analizza
Cerchio di curvatura
| Barra strumenti | Menu |
|---|---|
|
|
Analizza Cerchio di curvatura |
Il comando Curvatura valuta la curvatura di una curva o superficie su un punto usando il raggio di un cerchio.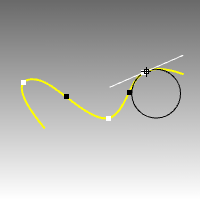
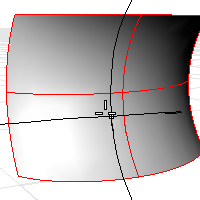
Le seguenti informazioni di valutazione della superficie vengono visualizzate nell'area comandi:
| Opzione da linea di comando | |
|---|---|
|
SegnaCurvatura |
Colloca un oggetto punto ed il cerchio di curvatura o i mezzi cerchi sul punto valutato sulla curva. In questo modo, si ottiene un riscontro permanente quando il raggio di curvatura è infinito (la curvatura è zero, la curva è localmente piana, per esempio ai punti di flesso in cui la curvatura cambia da un lato all'altro) e non può essere valutato. Questo metodo non automatizza il rintracciamento dei punti di flesso, ma permette di marcarli manualmente. |
| Barra strumenti | Menu |
|---|---|
|
|
Analizza Superfici > Analisi di curvatura |
Il comando AnalisiCurvatura valuta visivamente la curvatura di una superficie usando l'analisi in falsi colori.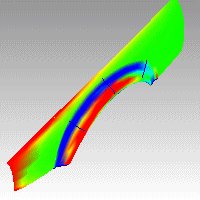
Curvatura
| Opzioni di stile | |
|---|---|
|
Gaussiana |
Nelle immagini sottostanti, il colore rosso viene assegnato a un valore positivo della curvatura Gaussiana, il verde viene assegnato a un valore della curvatura Gaussiana pari a zero ed il blu a un valore della curvatura Gaussiana negativo. Tutti i punti sulla superficie i cui valori di curvatura cadono all'interno dell'intervallo specificato verranno mostrati sullo schermo con il colore corrispondente. Per esempio, i punti con un valore di curvatura che cade giusto a metà dell'intervallo specificato saranno verdi. I punti sulla superficie con un valore di curvatura al di sotto dell'estremo rosso dell'intervallo saranno rossi, mentre i punti con un valore di curvatura al di sotto dell'estremo blu dell'intervallo saranno blu. Curvatura positivaUn valore positivo di curvatura Gaussiana corrisponde ad una superficie concava. Curvatura negativaUn valore negativo di curvatura corrisponde ad una superficie convessa. Curvatura pari a zeroUn valore pari a zero significa che la superficie è piatta almeno in una direzione. (Piani, cilindri e coni hanno una curvatura Gaussiana pari a zero). Se sapete qual è l'intervallo dei valori della curvatura che desiderate analizzare, inserite i valori nelle caselle editabili a fianco degli intervalli rosso e blu dell'"arcobaleno". I valori inseriti per il rosso devono essere diversi dai valori inseriti per il blu; i valori per il rosso possono essere più lunghi o più corti di quelli per il blu. |
|
Media |
Mostra il valore assoluto della curvatura media. Questa opzione è utile per trovare zone di variazioni brusche sulla superficie della curvatura. |
|
Raggio min. |
Se volete eseguire l'offset di una superficie di distanza r oppure tagliare in lamine una superficie con una sfera di raggio r, tutti i punti sulla superficie che "si curvano" con un raggio minore di r daranno dei problemi. L'offset diventerà un rompicapo. Nel caso del taglio in lamine, la sfera eliminerà del materiale che non desiderate eliminare. In questi casi, occorre porsi la domanda: "Questa superficie presenta alcune zone in cui si piega troppo bruscamente?". L'opzione Raggio min. vi aiuterà a rispondere a questa domanda. ROSSO = r BLU = 1.5 x r Se sulla superficie compare il colore rosso, in corrispondenza di quella zona non potrete eseguire un offset o un taglio a lamina. Normalmente ciò non succede invece con le zone blu. Le zone che vanno dal verde al rosso possono in alcuni casi risultare problematiche, per cui siate cauti. |
|
Raggio max. |
Questa opzione è utile per individuare le zone piane. Impostare un valore per il blu abbastanza alto (10->100->1000) ed un valore per il rosso tendente all'infinito. Le zone rosse presenti nel modello indicano i punti in cui la curvatura è praticamente uguale a zero. |
| Opzioni dell'intervallo di curvatura | |
|---|---|
|
Automatico |
Il comando AnalisiCurvatura analizza la curvatura della superficie usando la mappatura in falsi colori. Occorre mappare i valori ai colori saturati del computer. Per iniziare, usare l'opzione Automatico e quindi regolare i valori in modo tale che siano simmetrici ma con dimensioni paragonabili a quelle selezionate da Automatico. Il comando AnalisiCurvatura vi ricorda le impostazioni usate nell'ultima analisi di superficie realizzata. Se avete cambiato di molto la geometria di una superficie o avete cambiato superficie, è probabile che i valori precedentemente usati non siano appropriati. In qualsiasi caso, potete usare Automatico per calcolare automaticamente il valore di curvatura, per poi eseguire una mappatura con una corretta distribuzione del colore. |
|
Massimo |
Usare questa opzione se si desidera che la curvatura massima venga mappata in rosso e che la curvatura minima venga mappata in blu. Sulle superfici con una variazione di curvatura estrema, il risultato sarà probabilmente un'immagine poco informativa. |
|
Mostra isocurva |
Mostra la isocurve sugli oggetti. |
|
Aggiungi oggetti |
Attiva l'analisi di curvatura degli oggetti aggiuntivi selezionati. |
|
Rimuovi oggetti |
Disattiva l'analisi di curvatura degli oggetti selezionati. |
| Barra strumenti | Menu |
|---|---|
|
|
|
Il comando AnalisiCurvaturaOff chiude la finestra di dialogo Curvatura e disattiva la visualizzazione dell'analisi di curvatura.
| Barra strumenti | Menu | Alias |
|---|---|---|
|
|
Analizza Curve > Attiva grafico di curvatura |
COn |
Il comando GraficoCurvatura valuta visivamente la curvatura di una superficie usando un grafico.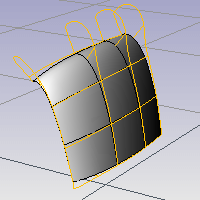
| Opzioni di analisi delle curve | |
|---|---|
|
Tangente |
Anche se gli span (tratti) della curva sono tangenti tra di loro, il grafico di curvatura cambia improvvisamente da un valore ad un altro. Gli span di una curva di grado 2 sono G1 oppure solo tangenti. Non hanno continuità di curvatura. |
|
Con continuità di curvatura |
Nel grafico di curvatura non ci sono interruzioni. Il grafico di curvatura del primo span si collega con l'estremo del grafico di curvatura del secondo span. La curva è di raccordo continua o G2 lungo gli span, visto che la sua curvatura non passa improvvisamente da un valore all'altro. Tuttavia, il grafico di curvatura del primo span non si sviluppa allo stesso ritmo del grafico del secondo span. Per cui, anche se la curvatura rimane la stessa, il tasso della curvatura cambia improvvisamente. |
Per capire meglio questo concetto, eseguire il comando Curvatura ed osservare il cerchio osculatore mentre si sposta lungo le curve.
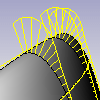
Grafico di curvatura
Imposta la dimensione delle linee indicatrici del grafico. Ricordate che la scala delle variazioni può essere esagerata di molto. Le variazioni della curvatura non dovrebbero essere più spesse di una mano di vernice. Una Scala impostata su 100 significa una scala di curvatura pari a 1:1.

Imposta il numero di linee indicatrici.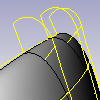
Mostra i vettori superficie soltanto nella direzione u.
Il campione di colore imposta il colore dei vettori.
Mostra i vettori superficie soltanto nella direzione v.
Il campione di colore imposta il colore dei vettori.
Attiva l'analisi del grafico di curvatura degli oggetti aggiunti alla selezione.
Disattiva l'analisi del grafico di curvatura degli oggetti selezionati.
| Barra strumenti | Menu | Alias |
|---|---|---|
|
|
Analizza Curve > Disattiva grafico di curvatura |
COff |
Il comando GraficoCurvaturaOff disattiva la visualizzazione del grafico di curvatura.
Per capire la nozione di curvatura gaussiana di un punto su una superficie, occorre innanzitutto sapere cos'è la curvatura di una curva.
In qualsiasi punto di una curva sul piano, la linea che si avvicina di più alla curva che attraversa questo punto è la linea tangente. Possiamo anche trovare il cerchio che si avvicina di più, che attraversi questo punto e che sia tangente alla curva. Il reciproco del raggio di questo cerchio è la curvatura della curva in questo punto.
Il cerchio che si avvicina di più si può trovare sulla destra o sulla sinistra della curva. Considerando questo fatto, possiamo per esempio assegnare un segno positivo alla curvatura se il cerchio si trova sulla sinistra della curva ed attribuirle un segno negativo se il cerchio si trova sulla destra della curva. Si parla di curvatura con segno.
Una generalizzazione della curvatura applicata alle superfici è la curvatura della sezione normale. Dato un punto sulla superficie ed una direzione situata sul piano tangente della superficie in quel punto, la curvatura della sezione normale viene calcolata intersecando la superficie con il piano suddiviso dal punto, la normale alla superficie in quel punto e la direzione. La curvatura della sezione normale è la curvatura con segno di questa curva nel punto preso in considerazione.
Se guardiamo in tutte le direzioni sul piano tangente alla superficie nel punto analizzato e calcoliamo la curvatura della sezione normale in tutte le direzioni, otterremo un valore massimo ed un valore minimo.
La curvatura gaussiana di una superficie in un punto è il prodotto delle curvature principali in quel punto. Il piano tangente di qualsiasi punto con una curvatura gaussiana positiva tocca la superficie in un solo punto, mentre il piano tangente di qualsiasi punto con una curvatura gaussiana negativa taglia la superficie. Qualsiasi punto con una curvatura media pari a zero ha una curvatura gaussiana negativa o pari a zero.
Le curvature principali di una superficie in un punto rappresentano il minimo ed il massimo delle curvature normali in quel punto. (Le curvature normali sono le curvature delle curve sulla superficie situate su piani che includono il vettore tangente in un dato punto). Le curvature principali si usano per calcolare la curvatura gaussiana e media di una superficie.
La curvatura media di una superficie in un punto è la metà della somma delle curvature principali in quel punto. Qualsiasi punto con una curvatura media pari a zero ha una curvatura gaussiana negativa o pari a zero.
Le superfici con una curvatura media ovunque pari a zero sono dette superfici minime. Le superfici con una curvatura media ovunque costante sono conosciute come superfici CMC (a curvatura media costante).
Le superfici CMC hanno la stessa curvatura media su tutta la superficie.
I processi fisici che si possono modellare con superfici CMC comprendono la formazione di bolle di sapone, sia libere che attaccate agli oggetti. Una bolla di sapone, diversamente da una semplice pellicola, racchiude un volume ed esiste in uno stato di equilibrio, dove la pressione leggermente maggiore all'interno della bolla viene equilibrata dalle forze della superficie minima della bolla stessa.
Le superfici minime sono il sottoinsieme delle superfici CMC, in cui la curvatura è ovunque zero.
I processi fisici che si possono modellare con superfici minime comprendono la formazione di pellicole di sapone che si estendono su oggetti fissi, come per esempio un cappio a filo metallico. Una pellicola di sapone non viene deformata dalla pressione dell'aria (che è uguale da entrambi i lati) ed è libera di minimizzare la propria area. Una bolla di sapone, invece, racchiude una quantità fissa di aria ed ha pressioni diverse al suo interno ed al suo esterno.
Rhinoceros 6 © 2010-2017 Robert McNeel & Associates. 18-dic-2017