과정
- 서피스 또는 메쉬 법선을 검사/수정하려면 Dir 명령을 사용합니다.

여섯 개의 직사각형 서피스 또는 방향이 정확한 메쉬 면이 상자의 체적을 정의합니다.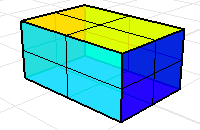
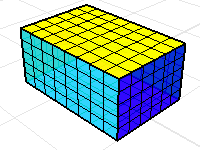
상자의 윗면이 없으면 체적 질량 속성 명령의 결과는 무의미합니다.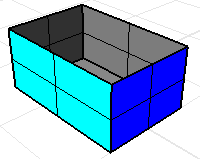

체적 명령의 일부로 선택된 개체는 반드시 체적을 가져야 합니다. 이를 확인하는 가장 간단한 방법은 솔리드 개체(닫힘, 다양체, 법선 방향이 바깥쪽을 향함)를 선택하는 것입니다. 그러나 개체를 폴리서피스 또는 메쉬로 결합하기에 어려운 경우가 있습니다.
이 경우, 체적 질량 속성은 솔리드가 아닌 개체의 모음으로 계산됩니다.
다음의 사항들을 반드시 확인해야 합니다:





폴리서피스 또는 각 가장자리의 메쉬는 최대한 두 개의 면이 공유하며, 이를 다양체(manifold)라고 합니다. 체적 질량 속성 명령은 모든 면의 체적이 경계로 둘러싸여 있다고 가정합니다.
각 서피스의 경계가 체적을 둘러싸고 있지 않은 비다양체 폴리서피스. 체적 질량 속성 명령의 결과는 무의미한 대답입니다.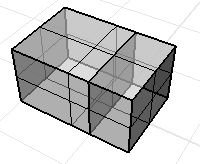
각 서피스의 경계가 체적을 둘러싸고 있는 비다양체 폴리서피스. 체적 질량 속성 명령의 결과가 유효합니다.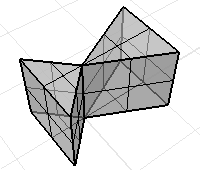
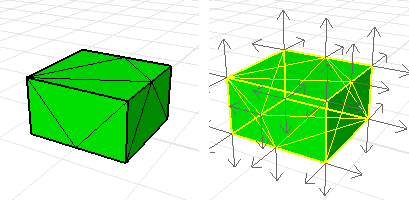
면에서 폴리서피스 또는 메쉬의 방위가 면에서 일관성이 없을 수도 있습니다.
Dir 명령을 사용하여 면의 법선을 표시합니다. 올바르게 방향이 지정된 솔리드의 법선은 바깥쪽을 향합니다.
이 메쉬의 법선이 일정하지 않습니다.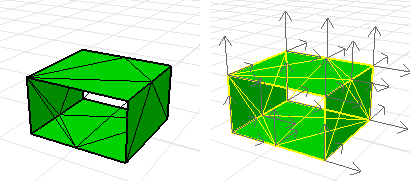
분야와 교재에 따라 각각의 모멘트의 정의에 사용하는 용어법과 기수법이 다르거나 때로는 상호 모순된 경우도 있습니다. 면적 모멘트 보고서의 정보로 어느 모멘트도 계산할 수 있으나, 필요한 모멘트를 얻기 위해 면적 모멘트 보고서의 여러 값을 합쳐 계산해야 하는 경우도 있습니다.
모서리가 0,0,0와 6,10,0인, 일정한 z평면의 면적 모멘트의 보고서를 다음과 같이 표시합니다.
면적 = 60 (+/- 1e-008)
면적 중심 = 3,5,0 (+/- 1e-009,1e-009,0)
면적 모멘트:
1차 모멘트
x: 180 (+/- 1e-007)
y: 300 (+/- 1e-007)
z: 0 (+/- 0)
2차 모멘트
xx: 720 (+/- 1e-007)
yy: 2000 (+/- 1e-006)
zz: 0 (+/- 0)
곱 모멘트
xy: 900 (+/- 1e-007)
yz: 0 (+/- 0)
zx: 0 (+/- 0)
절대좌표축에 대한 관성 면적 모멘트
Ix: 2000 (+/- 1e-006)
Iy: 720 (+/- 1e-007)
Iz: 2720 (+/- 1e-006)
절대좌표축에 대한 면적 회전 반경
Rx: 5.77350269 (+/- 1e-009)
Ry: 3.46410162 (+/- 1e-009)
Rz: 6.73300329 (+/- 1e-009)
중심좌표축에 대한 관성 면적 모멘트
Ix: 500 (+/- 1e-007)
Iy: 180 (+/- 1e-007)
Iz: 680 (+/- 1e-007)
중심좌표축에 대한 면적 회전 반경
Rx: 2.88675135 (+/- 1e-009)
Ry: 1.73205081 (+/- 1e-009)
Rz: 3.36650165 (+/- 1e-009)
괄호 안의 숫자는 계산의 정확도를 표시합니다.
면적 모멘트와 체적 모멘트 보고서에 있는 값의 정확한 묘사는 다음과 같습니다.
면적의 1차 모멘트의 단위는 길이3의 단위입니다. 체적의 1차 모멘트의 단위는 길이4입니다. xy 평면에 있는 면적의 1차 모멘트에 대하여 Mx를 "1차 모멘트 y:" 값으로 표시하는 분야와 교재도 있으나, 반대로 같은 기호를 "1차 모멘트 x:"의 값으로 표시하는 분야와 교재도 있습니다. My의 기호에 대해서도 마찬가지입니다.
적분에 의한 면적의 1차 모멘트의 정의는 다음과 같습니다:
면적 1차 모멘트 x: 값 = 면적 적분 x dA
면적의 1차 모멘트 y: 값 = 면적 적분 y dA
면적의 1차 모멘트 z: 값 = 면적 적분 z dA
이와 유사하게, 체적 1차 모멘트의 정의는 다음과 같습니다:
체적 1차 모멘트 x: 값 = 체적 적분 x dV
체적 1차 모멘트 y: 값 = 체적 적분 y dV
체적 1차 모멘트 z: 값 = 체적 적분 z dV
면적 또는 체적의 1차 모멘트와 면적 또는 체적, 면적 중심의 관계:
중심 x 좌표 = (1차 모멘트 x: 값)/M
중심 y 좌표 = (1차 모멘트 y: 값)/M
중심 z 좌표 = (1차 모멘트 z: 값)/M
M은 면적 또는 체적을 뜻합니다.
면적의 2차 모멘트는 길이4의 단위입니다. 체적의 2차 모멘트의 단위는 길이5의 단위입니다.
적분에 의한 면적의 2차 모멘트의 정의는 다음과 같습니다:
면적의 2차 모멘트 xx: 값 = 면적 적분x2 dA
면적의 2차 모멘트 yy: 값 = 면적 적분y2 dA
면적의 2차 모멘트 zz: 값 = 면적 적분z2 dA
이와 유사하게 체적의 2차 모멘트의 정의는 다음과 같습니다:
체적의 2차 모멘트 xx: 값 = 체적 적분 x2 dV
체적의 2차 모멘트 yy: 값 = 체적 적분y2 dV
체적의 2차 모멘트 zz: 값 = 체적 적분 z2 dV
면적의 곱 모멘트의 단위는 길이4의 단위입니다. 체적의 곱 모멘트의 단위는 길이5의 단위입니다.
적분에 의한 면적의 곱 모멘트의 정의는 다음과 같습니다:
면적의 곱 모멘트 xy: 값 = 면적 적분 xy dA
면적의 곱 모멘트 yz: 값 = 면적 적분 yz dA
면적의 곱 모멘트 zx: 값 = 면적 적분 zx dA
이와 유사하게, 체적의 곱 모멘트의 정의는 다음과 같습니다:
체적의 곱 모멘트 xy: 값 = 체적 적분 xy dV
체적의 곱 모멘트 yz: 값 = 체적 적분 yz dV
체적의 곱 모멘트 zx: 값 = 체적 적분 zx dV
면적 또는 체적의 관성곱은 좌표축에 평행하지 않은 축의 관성 모멘트의 계산에 사용할 수 있습니다. 보다 상세히 설명하자면, 어떤 축 중심의 관성 면적 모멘트는 면적, 면적의 1차 모멘트, 면적의 2차 모멘트, 그리고 면적의 곱 모멘트의 1차 결합으로 구할 수 있습니다.
관성 면적 모멘트의 단위는 길이4의 단위입니다. 관성 체적 모멘트의 단위는 길이5의 단위입니다. Ix, Iy, Iz의 기호를 사용하여 절대좌표의 x축, y축, z축 중심의 관성 면적 모멘트를 표시하는 것이 표준화되어 있습니다.
적분에 의한 절대좌표축에 대한 관성 면적 모멘트의 정의는 다음과 같습니다:
Ix= 면적 적분 (y2+ z2) dA
Iy= 면적 적분 (z2+ x2) dA
Iz= 면적 적분 (x2+ y2) dA
관성 체적 모멘트도 유사하게 정의됩니다.
2차 모멘트에 의한 절대좌표축 중심의 관성 면적 모멘트 또는 관성 체적 모멘트의 정의는 다음과 같습니다.
Ix = 2차 모멘트 yy: 값 + 2차 모멘트 zz: 값,
Iy = 2차 모멘트 zz: 값 + 2차 모멘트 xx: 값,
Iz = 2차 모멘트 xx: 값 + 2차 모멘트 yy: 값.
회전 반경의 단위는 길이의 단위입니다. 공학의 참고서와 교재에서는 회전 반경을 R 또는 k의 기호로 표시합니다. 3D 축 중심의 면적 회전 반경은 (축 중심의 관성 면적 모멘트/면적)의 제곱근으로 정의됩니다.
이와 유사하게, 체적 회전 반경은 (축 중심의 관성 체적 모멘트)/체적)의 제곱근으로 정의됩니다.
면적 모멘트의 보고서에 있는 절대 좌표축 중심의 면적 회전 반경 또는 체적 회전 반경의 계산 방법은:
Rx = sqrt( Ix / M ),
Ry = sqrt( Iy / M ),
Rz = sqrt( Iz / M ),
M은 면적 또는 체적을 뜻합니다.
여기서의 Ix, Iy, Iz는 절대좌표축 중심의 관성 모멘트입니다.
중심좌표축에 대한 관성 면적 모멘트의 단위는 길이4의 단위입니다. 중심좌표축에 대한 관성 체적 모멘트의 단위는 길이5의 단위입니다. Ix, Iy, Iz의 기호를 사용하여 관성 면적 모멘트를 표시하는 것이 표준화되어 있습니다.
적분에 의한 개체의 중심좌표축에 대한 관성 모멘트의 정의는 다음과 같습니다:
Ix = 면적 적분 ((y-y0)2 +( z-z0)2) dA
Iy = 면적 적분 ((z-z0)2 +( x-x0)2) dA
Iz = 면적 적분 ((x-x02 + (y-y0)2) dA
여기서 (x0>, y0, z0) 는 면적 중심입니다.
체적 중심에 대한 관성 체적 모멘트도 유사한 방법으로 정의됩니다.
관성 면적(또는 체적) 모멘트를 2차 모멘트, 1차 모멘트, 면적(또는 체적)으로 표현하면 다음과 같습니다:
Ix = 2차 모멘트 yy: 값
+ 2차 모멘트 zz: 값
- 2*y0*(1차 모멘트 y: 값)
- 2*z0*(1차 모멘트 z: 값)
+ (y02+z02)*M,
Iy = 2차 모멘트 zz: 값
+ 2차 모멘트 xx: 값
- 2*z0*(1차 모멘트 z: 값)
- 2*x0*(1차 모멘트 x: 값)
+ (z02+x02)*M,
Iz = 2차 모멘트 xx: 값
+ 2차 모멘트 yy: 값
- 2*x0*(1차 모멘트 x: 값)
- 2*y0*(1차 모멘트 y: 값)
+ (x02+y02) *M,
M은 면적 또는 체적을 뜻합니다.
중심좌표축에 대한 면적 회전 반경의 단위는 길이의 단위입니다. 모멘트의 보고서에 있는 중심좌표축에 대한 면적(또는 체적) 회전 반경의 계산 방법은 다음과 같습니다.
Rx = sqrt( Ix / M ),
Ry = sqrt( Iy / M ),
Rz = sqrt( Iz / M ),
M은 면적 또는 체적을 뜻합니다.
여기서 Ix, Iy, and Iz 는 면적 또는 체적 중심에 대한 관성의 면적 (또는 체적) 모멘트입니다.
개체의 면적 중심을 보고하고 표시합니다.
개체의 관성 면적 모멘트를 보고합니다.
서피스와 폴리서피스의 체적 중심을 좌표로 보고하고, 그 위치에 점 개체를 배치합니다.
서피스와 폴리서피스의 관성의 체적 모멘트를 보고합니다.
Rhinoceros 6 © 2010-2020 Robert McNeel & Associates. 2020-12-08