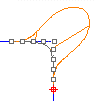
Die Stetigkeit einer Kurve oder Fläche kann mit Gn angegeben werden, wobei ein größeres n einer glatteren Kurve oder Fläche entspricht. Dabei gilt bei Betrachtung der Segmente auf den beiden Seiten eines Punktes auf einer Kurve:
Siehe auch: Wikipedia: Geometrische Stetigkeit
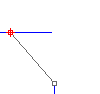
Bei der Positionsstetigkeit (G0-Stetigkeit) wird nur die Position in Betracht gezogen. Wenn sich die Endpunkte der beiden Kurven an der gleichen Stelle im Raum befinden, sind die Kurven an den Enden positionsstetig (G0). Die beiden Kurven berühren sich also an ihren Endpunkten. 
Bei der tangentialen Stetigkeit (G1-Stetigkeit) werden Position und Kurvenrichtung an den Enden gemessen. Die beiden Kurven berühren sich also nicht nur, sondern weisen am Punkt, an dem sie sich berühren, die gleiche Richtung auf.
Die Richtung wird durch den ersten und zweiten Punkt auf jeder der beiden Kurven bestimmt. Wenn diese zwei Punkte auf eine Linie fallen, sind die beiden Kurven an den Enden tangential.
Die erste Ableitung der beiden Kurven ist an dem Punkt gleich, an dem sie sich berühren.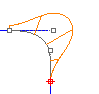
Bei der Krümmungsstetigkeit (G2-Stetigkeit) werden zwischen zwei Kurven die Position, Richtung und der Krümmungsradius an den Enden berechnet. Wenn der Krümmungsradius am gemeinsamen Endpunkt gleich ist, sind die Kurven krümmungsstetig (G2). Die Kurven gehen also an der Stelle, an der sie aufeinander treffen, nicht nur in die gleiche Richtung, sondern haben an diesem Punkt auch den gleichen Radius. Diese Bedingung kann nicht einfach dadurch bestimmt werden, indem die Position der Punkte betrachtet wird.
Die ersten und zweiten Ableitungen der Gleichungen sind an diesem Punkt gleich.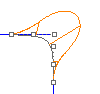
G3-Stetigkeit fügt eine dritte Bedingung hinzu: planare Beschleunigung. Kurven, die G3-stetig sind, berühren einander, gehen in die gleiche Richtung, haben den gleichen Radius und dieser Radius wird an einem gewissen Punkt mit der gleichen Rate beschleunigt.
Bei G3-stetigen Kurven sind auch die dritten Ableitungen der beiden Segmente gleich.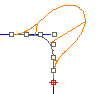
G4-Stetigkeit wird selten verwendet, kann aber in bestimmten Einzelfällen wichtig sein. G4-stetige Kurven weisen die gleichen Bedingungen auf wie G3-Kurven, wobei ihre Krümmungsbeschleunigung in drei Dimensionen gleich ist.