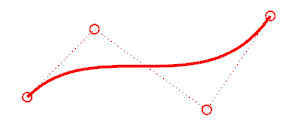
Las operaciones de edición descritas en esta sección permiten dividir objetos, hacer agujeros y unir objetos. Algunos de estos comandos unen curvas con curvas o superficies con superficies o polisuperficies. Otros permiten dividir una curva o polisuperficie compuesta en sus componentes.
Los comandos Unir, Descomponer, Recortar y Partir se pueden usar en curvas, superficies y polisuperficies.
Los comandos Reconstruir, CambiarGrado y Suavizar modifican la forma de una curva o superficie cambiando su estructura de puntos de control subyacente.
Además, los objetos tienen propiedades asignadas, tales como color, capa, material de renderizado y otros atributos según el objeto. El comando Propiedades permite administrar estas propiedades.
El comando Unir conecta curvas o superficies formando un objeto. Por ejemplo, una policurva puede estar formada por segmentos de línea, arcos, polilíneas y curvas de forma libre. El comando Unir también une las superficies adyacentes formando una polisuperficie.
El comando Descomponer deshace la conexión entre las curvas o superficies unidas. En polisuperficies, este comando es útil si desea editar cada superficie individualmente con puntos de control.
Los comandos Recortar y Partir son similares. La diferencia es que al recortar un objeto, se seleccionan las partes y se eliminan. Cuando se parte un objeto, ambas partes permanecen en el objeto.
El comando Partir puede dividir una superficie con una curva, una superficie, una polisuperficie o sus mismas curvas isoparamétricas.
El comando DeshacerRecorte deshace la curva de corte de una superficie, con la opción de mantener la curva para volver a utilizarla.
Pueden realizarse cambios sutiles en la forma de una curva o superficie moviendo la posición de sus puntos de control. Rhino dispone de varias herramientas para la edición de puntos de control. Algunos comandos, tales como Reconstruir, Alisar y Suavizar, ofrecen algunas soluciones automáticas para redistribuir los puntos de control sobre una curva o superficie. Otros comandos, como el arraste y toque ligero de puntos de control,y Manejadores, permiten controlar manualmente la posición de los puntos de control individuales o en grupo.
Para editar curvas y superficies manipulando los puntos de control, utilice el comando ActivarPuntos para activar los puntos de control.
Cuando termine de editar los puntos de control, utilice el comando DesactivarPuntos o pulse Esc para desactivarlos.
Los puntos de control en polisuperficies no se pueden activar para editar. Editar los puntos de control de las polisuperficies podría separar los bordes de las superficies unidas creando "agujeros" en la polisuperficie.
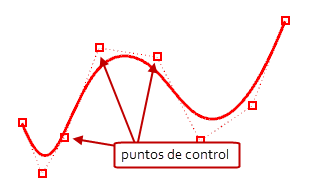
Cuando se mueven puntos de control, la curva o superficie cambia y Rhino la redibuja suavemente. La curva o superficie no se dibuja a través de los puntos de control, sino que es atraída a las nuevas posiciones de los puntos de control. Esta acción permite que el objeto se deforme suavemente. Cuando los puntos de control están activados, puede utilizar los comandos de transformación de Rhino para manipular los puntos. También es posible reconstruir superficies para añadir puntos de control y redistribuirlos.
Añadir puntos de control a una curva proporciona más control sobre la forma de la curva. La manipulación de los puntos de control también permite eliminar puntos de torsión, uniformizar curvas y añadir o quitar detalles. La tecla Eliminar elimina los puntos de control de las curvas. La eliminación de puntos de control modifica la forma la curva.
Un polinomio es una función del tipo y = 3x3 –2x +1. El "grado" del polinomio es la mayor potencia de la variable. Por ejemplo, el grado de 3 ·x 3 –2 ·x + 1 es 3; el grado de –x 5 + x 2 es 5, y así sucesivamente. Las funciones NURBS son polinomios racionales y el grado de las NURBS es el grado del polinomio. Desde el punto de vista de un modelado NURBS, el grado -1 es el número máximo de "curvaturas" que puede haber en cada segmento.
Por ejemplo:
Una curva de grado 1 debe tener al menos dos puntos de control.
Una línea tiene menos de grado 1. No tiene ninguna curvatura.

Una curva de grado 2 debe tener 3 puntos de control como mínimo.
Una parábola, una hipérbola, un arco y un círculo (curvas de sección cónica) tienen menos de grado 2. Tienen una curvatura.
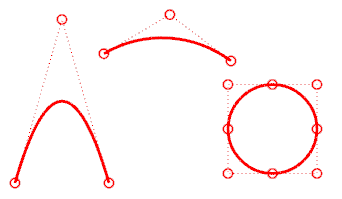
Una curva de grado 3 debe tener al menos cuatro puntos de control.
Una Bézier cúbica tiene menos de grado 3. Si se disponen sus puntos de control en forma de zig-zag, se obtienen dos curvaturas.