Curvature
|
|
Curvatureコマンド
曲線またはサーフェス上の指定した点での曲率の値を円の半径を使用して評価します。
操作手順
曲線を選択します。
マーカーのある位置での曲線の曲率半径がステータスバーに表示され、曲率と同じ半径の黒い円がマーカーの位置で曲線に接して表示されます。曲線の接線も白く表示されます。
曲線の曲率が点から両方向に下がり始める部分に、白い点で最大曲率点が示されます。
曲率円が曲線の1つの側から反対側へ移るところに、黒い点で最小曲率点が示されます。黒い点での曲率は常に0です。
曲率情報を得たい位置でピックするか、Escキーを押してコマンドを終了します。
サーフェスの曲率を分析するには
サーフェスを選択します。
カーソルを動かすとカーソルの位置に2つの半円が現れ、その点での最小と最大の曲率を示します。
サーフェス上の点をピックします。
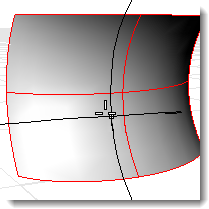
次のサーフェス評価情報がコマンド領域に表示されます。
パラメータ位置でのサーフェス曲率評価
3D点
3D法線
最大および最小主曲率
ガウス曲率
平均曲率
メモ
滑らかな曲線上にあるすべての点には、その曲線のその地点での曲率を最も正確に近似した円があります。
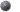カーソルは自動的に曲線の変曲点（曲率の正、負が変わるところ）にスナップします。
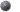同様に、滑らかなサーフェスにあるすべての点にも2つの曲率近似の円があります。半径が一番大きい円は半径が一番小さい円と直交します。
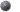主曲率円弧の半径の逆数です。
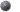ガウス曲率は、両方の半円が同じ方向を向いている場合は正の値で、反対方向を向いている場合は負の値になります。一方の半円が直線の場合、ガウス曲率は0になります。
オプション
曲率カーブ作成
点オブジェクトと、曲率の円（曲線の場合）または曲率の半円（サーフェスの場合）をピックした点で作成します。
曲率半径が無限大の場合（曲率が0。曲線が局部的に平らである。例えば、曲線の湾曲が急激に反対に変わる変曲点など。）、それを知らせるメッセージが表示され、曲率は評価されません。これによって自動的に変曲点を見つけることはできませんが、手動で印を付けることができます。
サーフェス上の点におけるガウス曲率を理解するには、まず曲線の曲率について理解しなければなりません。
平面上の曲線のどの点をとってみても、その点を通り、その点で曲線を最もよく近似する線を接線と呼びます。また、曲線に接し、その点を通る形状を最もよく近似する円を求めることもできます。この円の半径の逆数がその点における曲線の曲率です。
曲線を最もよく近似する円は曲線の右側にある場合も左側にある場合もあります。この区別が重要な場合は、慣例として円が左側にある場合はその曲率を正の曲率とみなし、右側にある場合は負の曲率とみなします。これが正負の符号のついた曲率ということになります。
曲率を一般化してサーフェスにも当てはめる概念として法曲率があります（英語でNormal section curvature 、法断面曲率ともいいます）。サーフェス上の点、その点を通る接触平面、そしてその平面上に特定の方向にその点から伸びる線を考えてみましょう。点、方向、そしてその点でのサーフェスの法線で定義する平面がサーフェスと交差するところで断面曲線が定義されます。分析したい点でのこの曲線の正または負の曲率が法曲率です。
分析したいサーフェス上の点の接触平面のあらゆる方向での法曲率を計算すれば、最大値と最小値が必ずあります。
ガウス曲率
サーフェス上の点におけるガウス曲率はその点での主曲率の積です。正のガウス曲率がある点での接触平面はサーフェスと1 点でしか接触しませんが、負のガウス曲率がある点での接触平面はサーフェスを分割します。平均曲率がゼロの点はガウス曲率の値がゼロか負の値です。
主曲率
特定の点における法曲率の最大値と最小値はサーフェスのその点における主曲率です。（法曲率は特定の点からの接線ベクトルと法線で定義される平面上にある、サーフェス上の曲線の曲率です。）この主曲率はサーフェスのガウス曲率と平均曲率の計算に使用されます。
平均曲率
サーフェス上の点における平均曲率はその点での主曲率の和の半分です。平均曲率がゼロの点はガウス曲率の値がゼロか負の値です。
あらゆる点で平均曲率がゼロのサーフェスは極小曲面といいます。あらゆる点での平均曲率の値が一定しているサーフェスは平均曲率一定曲面（CMC - Constant Mean Curvature Surface）と呼ばれることもあります。
平均曲率一定曲面はあらゆる点での平均曲率の値が一定しています。
平均曲率一定曲面でモデリングできる物理的プロセスの例としてシャボン玉（自由に飛んでいる場合や何かにくっついている場合）があります。単純な石けん膜と違って、シャボン玉は体積を持ち、外部より多少高いシャボン玉の内部の圧力と、シャボン玉自体の表面積を最も小さくしようとする力が釣り合っている状態にあります。
極小曲面は至るところの曲率がゼロの平均曲率一定曲面の中のサブセットです。
極小曲面でモデリングできる物理的プロセスの例として、固定された枠（針金の輪など）に張っている石けん膜があります。石けん膜は空気圧で変形されず（どちらの側に対する圧力も同じなので）、表面積を最も小さくする妨げはありません。これは一定の空気の量を持っていて内側と外側からの圧力が違うシャボン玉とは対照的です。
ツールバー
メニュー
ショートカット