Proprietà di massa del volume di oggetti chiusi/aperti

Gli oggetti selezionati all'interno del comando Volume devono delimitare un volume. Per assicurarsi che ciò avvenga, basta selezionare degli oggetti solidi (chiusi, manifold e con la direzione di tutte le superfici orientata verso l'esterno). In alcuni casi, tuttavia, non conviene unire gli oggetti in polisuperfici o mesh di questo tipo.

In tali casi, le proprietà di massa di un volume si possono calcolare a partire da un insieme di oggetti non solidi.

Occorre assicurarsi che:

Gli oggetti racchiudano un volume.

Ciascuna superficie si trovi sul limite del volume, non al suo interno.

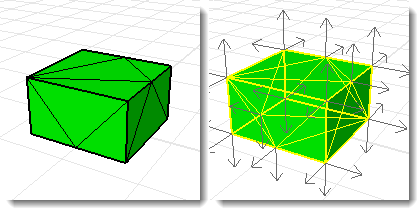
La normale delle superfici o mesh sia rivolta verso l'esterno rispetto al volume.

Passi

Si usi il comando Dir per verificare o modificare la normale delle superfici o mesh.

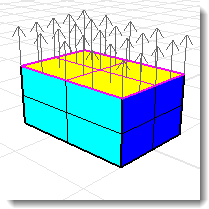
Sei superfici o facce mesh rettangolari con il corretto orientamento definiscono il volume della scatola.

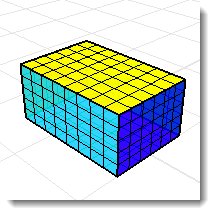
Senza la parte superiore della scatola, i comandi di proprietà di massa di un volume restituiscono un risultato senza senso.

Proprietà di massa del volume di oggetti non-manifold

Una polisuperficie o mesh in cui ciascun lato è condiviso da al massimo due facce è detta manifold. I comandi di proprietà di massa volume assumono che ciascuna faccia delimita il volume.

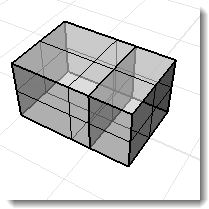
Una polisuperficie non-manifold in cui ciascuna superficie non delimita un volume. I comandi di proprietà di massa del volume restituiscono un risultato senza senso.

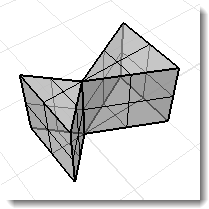
Polisuperficie non-manifold in cui ciascuna superficie delimita un volume. I comandi di proprietà di massa del volume restituiscono dei dati validi.

Proprietà di massa del volume di oggetti non orientati

Una polisuperficie o una mesh possono presentare delle facce orientate in modo incoerente.

Usare il comando Dir per visualizzare la direzione delle normali delle facce. Un solido correttamente orientato ha le normali rivolte verso l'esterno.

Questa mesh presenta delle normali incongruenti.

Per invertire la direzione delle normali di alcune facce di una polisuperficie

Usare il comando Esplodi o il comando EstraiSrf per isolare le facce problematiche.

Usare il comando Dir sulle singole facce per orientare correttamente le normali.

Usare il comando Unisci per ricostruire la polisuperficie.

Per modificare (uniformare) la direzione delle normali nelle mesh non orientate

Usare il comando UnificaNormaliMesh.

Mesh aggiustata con le normali coerenti e rivolte verso l'esterno.

Dettagli per il calcolo delle proprietà di massa

Diverse discipline e testi fanno riferimento a differenti, e talvolta contraddittorie, nomenclature e notazioni per definire i vari momenti. Le informazioni nel rapporto dei momenti dell'area o del volume possono essere utilizzate per il calcolo di ciascuno dei vari momenti. Per ottenere un momento specifico, potrebbe essere necessario combinare tra di loro i vari valori del rapporto dei momenti.

Esempio

Ad esempio, i momenti di area riportati per un piano z costante con angoli a 0,0,0 e 6,10,0 sono elencati di seguito.

Area = 60 (+/- 1e-008)

Centroide dell'area = 3,5,0 (+/- 1e-009,1e-009,0)

Momenti dell'area:

Primi momenti
x: 180 (+/- 1e-007)
y: 300 (+/- 1e-007)
z: 0 (+/- 0)

Secondi momenti
xx: 720 (+/- 1e-007)
yy: 2000 (+/- 1e-006)
zz: 0 (+/- 0)

Momenti del prodotto
xy: 900 (+/- 1e-007)
yz: 0 (+/- 0)
zx: 0 (+/- 0)

Momenti di inerzia dell'area rispetto agli assi del sistema di riferimento assoluto
Ix: 2000 (+/- 1e-006)
Iy: 720 (+/- 1e-007)
Iz: 2720 (+/- 1e-006)

Raggi di rotazione dell'area rispetto agli assi del sistema di riferimento assoluto
Rx: 5.77350269 (+/- 1e-009)
Ry: 3.46410162 (+/- 1e-009)
Rz: 6.73300329 (+/- 1e-009)

Momenti di inerzia dell'area rispetto agli assi del sistema di riferimento del centroide
Ix: 500 (+/- 1e-007)
Iy: 180 (+/- 1e-007)
Iz: 680 (+/- 1e-007)

Raggi di rotazione dell'area rispetto agli assi del sistema di riferimento del centroide
Rx: 2.88675135 (+/- 1e-009)
Ry: 1.73205081 (+/- 1e-009)
Rz: 3.36650165 (+/- 1e-009)

I numeri all’interno delle parentesi riportano l’accuratezza del calcolo.

Le descrizioni precise dei valori riguardanti i momenti dell'area e del volume sono riportate di seguito.

Primi momenti

I primi momenti dell'area hanno unità di lunghezza3. I primi momenti del volume hanno unità di lunghezza4. Quando si fa riferimento ai momenti dell'area nel piano xy, alcune discipline e testi utilizzano il simbolo Mx per indicare il valore riportato come "Primi momenti y:", mentre altri usano lo stesso simbolo per indicare il valore riportato come "Primi momenti x:". Una situazione analogamente confusa riguarda il simbolo My.

In termini di integrali, i primi momenti dell'area sono definiti come:

Primo momento area x: valore = integrale di x dA sull'area,

Primo momento area y: valore = integrale di y dA sull'area,

Primo momento area z: valore = integrale di z dA sull'area.

In modo simile, i primi momenti del volume sono definiti come:

Primo momento volume x: valore = integrale di x dV sul volume,

Primo momento volume y: valore = integrale di y dV sul volume,

Primo momento volume z: valore = integrale di z dV sul volume.

Sia per un'area che per un solido, la relazione tra i primi momenti, l'area o il volume ed il centroide dell'area è:

Coordinata x del centroide = (primo momento x: valore)/M,

Coordinata y del centroide = (primo momento y: valore)/M,

Coordinata z del centroide = (primo momento z: valore)/M,

dove M sta per l'area o il volume.

Secondi momenti

I secondi momenti dell'area hanno unità di lunghezza4. I secondi momenti del volume hanno unità di lunghezza5.

In termini di integrali, i secondi momenti dell'area sono definiti come:

Secondo momento area xx: valore = integrale di x2 dA sull'area.

Secondo momento area yy: valore = integrale di y2 dA sull'area.

Secondo momento area zz: valore = integrale di z2 dA sull'area.

In modo simile, i secondi momenti del volume sono definiti come:

Secondo momento volume xx: valore = integrale di x2 dV sul volume,

Secondo momento volume yy: valore = integrale di y2 dV sul volume,

Secondo momento volume zz: valore = integrale di z2 dV sul volume.

Momenti del prodotto

Il momenti del prodotto dell'area hanno unità di lunghezza 4. I momenti del prodotto del volume hanno unità di lunghezza 5.

In termini di integrali, i momenti del prodotto dell'area sono definiti come:

Momento prodotto area xy: valore = integrale di xy dA sull'area,

Momento prodotto area yz: valore = integrale di yz dA sull'area,

Momento prodotto area zx: valore = integrale di zx dA sull'area.

In modo simile, i momenti del prodotto del volume sono definiti come:

Momento prodotto volume xy: valore = integrale di xy dV sul volume,

Momento prodotto volume yz: valore = integrale di yz dV sul volume,

Momento prodotto volume zx: valore = integrale di zx dV sul volume.

Sia per un'area che per un volume, i prodotti di inerzia sono utili per calcolare i momenti di inerzia rispetto agli assi che non sono paralleli ad un asse coordinato. In particolare, il momento di inerzia di un'area rispetto ad un asse qualsiasi può essere espresso come una combinazione lineare dell'area, dei primi momenti dell'area, dei secondi momenti dell'area e dei momenti del prodotto dell'area.

Momenti di inerzia rispetto agli assi del sistema di riferimento assoluto

I momenti di inerzia dell'area hanno unità di lunghezza4. I momenti di inerzia del volume hanno unità di lunghezza 5. Lo standard di definizione impiega comunemente i simboli Ix, Iy e Iz per indicare i momenti di inerzia dell'area rispetto agli assi x, y e z assoluti.

In termini di integrali, i momenti di inerzia dell'area rispetto agli assi assoluti sono definiti come:

Ix = integrale di (y2 + z2) dA sull'area,

Iy = integrale di (z2 + x2) dA sull'area,

Iz = integrale di (x2 + y2) dA sull'area.

I momenti di inerzia del volume sono definiti in modo simile.

Sia per un'area che per un volume, i momenti di inerzia rispetto agli assi assoluti sono definiti in termini di secondi momenti come:

Ix = secondo momento yy: valore + secondo momento zz: valore,

Iy = secondo momento zz: valore + secondo momento xx: valore,

Iz = secondo momento xx: valore + secondo momento yy: valore.

Raggi di rotazione rispetto agli assi del sistema di riferimento assoluto

I raggi di rotazione hanno unità di lunghezza. La terminologia tecnica adotta frequentemente R o k per denotare i raggi di rotazione. Il raggio di rotazione dell'area rispetto ad un asse 3D viene definito dalla radice quadrata di (momento di inerzia dell'area rispetto all'asse)/area.

Analogamente, il raggio di rotazione del volume viene definito dalla radice quadrata di (momento di inerzia del volume rispetto all'asse)/volume.

Sia per un'area che per un volume, i raggi di rotazione lungo gli assi assoluti nel rapporto dei momenti dell'area sono calcolati come:

Rx = sqrt( Ix / M ),

Ry = sqrt( Iy / M ),

Rz = sqrt( Iz / M ),

dove M sta per l'area o il volume.

Ix, Iy e Iz rappresentano i momenti di inerzia dell'area rispetto agli assi assoluti.

Momenti di inerzia rispetto agli assi del sistema di riferimento del centroide

I momenti di inerzia dell'area rispetto al centroide hanno unità di lunghezza 4. I momenti di inerzia del volume rispetto al centroide hanno unità di lunghezza 5. Lo standard di definizione impiega comunemente i simboli Ix, Iy ed Iz per denotare questi momenti di inerzia dell'area.

In termini di integrali, i momenti di inerzia dell'area rispetto al centroide dell'area di un oggetto sono definiti come:

Ix = integrale di ((y-y0)2 +( z-z0)2) dA sull'area,

Iy = integrale di ((z-z0)2 +( x-x0)2) dA sull'area,

Iz = integrale di ((x-x0)2 + (y-y0)2) dA sull'area,

Dove (x0>, y0, z0) sono le coordinate del centroide dell'area.

I momenti di inerzia del volume rispetto al centroide del volume sono definiti in modo simile.

I momenti di inerzia dell'area (o volume) vengono espressi in termini di secondi momenti, primi momenti, ed area (o volume):

Ix = secondo momento yy: valore

+ secondo momento zz: valore

- 2*y0*(primo momento y: valore)

- 2*z0*(primo momento z: valore)

+ (y02+z02)*M,

Iy = secondo momento zz: valore

+ secondo momento xx: valore

- 2*z0*(primo momento z: valore)

- 2*x0*(primo momento x: valore)

+ (z02+x02)*M,

Iz = secondo momento xx: valore

+ secondo momento yy: valore

- 2*x0*(primo momento x: valore)

- 2*y0*(primo momento y: valore)

+ (x02+y02) *M,

dove M sta per l'area o il volume.

Raggi di rotazione rispetto agli assi del sistema di riferimento del centroide

I raggi di rotazione rispetto al centroide hanno unità di lunghezza. Per un'area o un volume, i raggi di rotazione rispetto al centroide nel rapporto dei momenti vengono calcolati nel seguente modo:

Rx = sqrt( Ix / M ),

Ry = sqrt( Iy / M ),

Rz = sqrt( Iz / M ),

dove M sta per l'area o il volume.

Qui Ix, Iy e Iz rappresentano i momenti di inerzia dell'area (o volume) rispetto al centroide dell'area o del volume.