AnálisisDeCurvatura
|
|
|
Superficie Análisis de curvatura |
|
AnálisisDeCurvatura
Calcula visualmente la curvatura de superficie utilizando el análisis de color falso.
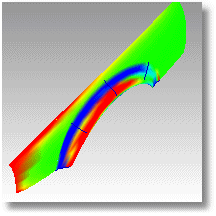
Estas herramientas se pueden utilizar para obtener información sobre el tipo y la cantidad de curvatura en una superficie. El análisis de curvatura gaussiana y media puede mostrar si y dónde hay anomalías en la curvatura de una superficie.
Los cambios repentinos como relieves, mellas, áreas planas, ondulaciones o, en general, áreas de curvatura que son superiores o inferiores que la superficie adyacente se pueden localizar y corregir si es necesario.
La visualización de curvatura gaussiana sirve para decidir si una superficie puede desarrollarse y convertirse en un patrón plano.
Una superficie suave tiene dos curvaturas principales. La curvatura gaussiana es producto de las curvaturas principales. La curvatura media es el promedio de las dos curvaturas principales.
Pasos
Seleccione objetos.
Defina el estilo y el intervalo.
Opciones
Gaussiana
En las imágenes inferiores, el rojo se asigna a un valor positivo de la curvatura gaussiana, el verde se asigna a la curvatura gaussiana de cero y, el azul, al valor negativo de la curvatura gaussiana.
Cualquier punto en la superficie con valores de curvatura entre los valores que especifique se mostrarán usando el color correspondiente. Por ejemplo, los puntos con un valor de curvatura a la mitad del valor especificado se verán verdes. Los puntos de la superficie que tengan valores de curvatura más allá de la punta final del área roja serán rojos y los puntos con valores de curvatura más allá del área azul serán azules.
Resultados
Curvatura positiva
El valor positivo de una curvatura Gaussiana significa que la superficie tiene forma de bol.
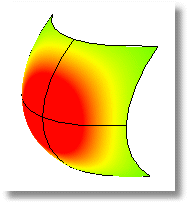
Curvatura negativa
Un valor negativo significa que la superficie tiene forma de silla de montar.
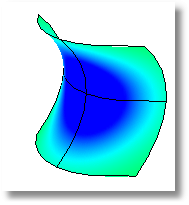
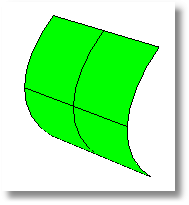
Curvatura cero
Un valor de cero significa que la superficie es plana al menos en una dirección. (Los planos, cilindros y conos tienen una curvatura gaussiana de cero).
Si conoce los intervalos de los valores de la curvatura que está interesado en analizar, introduzca dichos valores en los cuadros de edición al lado de las partes roja y azul del "arcoiris". Los valores que utilice para el color rojo deberían ser diferentes al valor utilizado para el azul, pero el valor para el rojo puede ser mayor o menor que el valor para el azul.
Opciones
Media
Muestra el valor absoluto de la curvatura media. Sirve para hallar áreas de cambio brusco en la curvatura de la superficie.
Radio máx
Esta opción es útil para la detección de puntos planos. Defina un valor más bien alto para el azul (10 > 100 > 1000) y cerca del infinito para el rojo. Las áreas rojas indicarán los puntos planos donde la curvatura es prácticamente cero.
Radio mín
Si quiere desfasar una superficie a una distancia r o quiere fresar una superficie con una bola de corte de radio r, cualquier parte de la superficie que se curve con un radio menor que r causará problemas.
En el caso de un desfase, obtendrá un objeto retorcido que se atraviesa a sí mismo. En el caso del fresado, la bola de corte eliminará el material que quiera mantener.
En estos casos, debe ser capaz de contestar a la pregunta "¿Esta superficie presenta alguna parte demasiado doblada?" La opción Radio mín debería ayudarle a responder esta pregunta.
ROJO = r AZUL = 1.5 x r
No se puede desfasar/fresar en ninguna parte roja de la superficie. Las áreas de color azul no presentan ningún problema. Sin embargo, debería desconfiar de las áreas de verde a rojo.
Intervalo automático
Con el uso del mapeado de color falso, el comando AnálisisDeCurvatura analiza la curvatura de superficie. Debe mapear los valores correspondientes a los colores saturados del ordenador. En un punto de inicio, utilice la opción Intervalo automático y ajuste los valores para que sean simétricos pero con magnitudes comparables a las seleccionadas por Intervalo automático.
El comando AnálisisCurvatura intenta recordar los parámetros utilizados la última vez que analizó una superficie. Si ha modificado totalmente la geometría de una superficie o ha cambiado a una nueva superficie, estos valores no serán adecuados. En este caso puede utilizar el comando Intervalo automático para calcular automáticamente un valor de curvatura en un mapeado de color que resultará en una buena distribución del color.
Intervalo máx
Escoja esta opción si desear que el máximo de curvatura se mapee en rojo y el mínimo en azul. En superficies con extrema variación de curvatura, esto puede dar lugar a una imagen que no proporciona ningún tipo de información.
Notas
Si cuando utiliza el comando AnálisisDeCurvatura, cualquiera de los objetos seleccionados no tiene una malla de análisis de superficie, se creará una malla invisible basada en los parámetros del cuadro de diálogo Opciones de malla poligonal.
Opciones de malla poligonal
Menos polígonos – Más polígonos
El botón deslizante controla aproximadamente la densidad y el número de mallas poligonales. Ajuste el control deslizante y haga clic.
La malla se dibuja como previsualización en las vistas y el cuadro de diálogo permanece en la pantalla por si necesita hacer más ajustes.
Las mallas de análisis de superficies se guardan en los archivos de Rhino. Estas mallas pueden ser grandes. El comando ActualizarSombreado y la opción Guardar sólo geometría de los comandos Guardar y GuardarComo eliminan las mallas de análisis de las superficies existentes.
Para analizar apropiadamente una superficie NURBS de forma libre, el comando de análisis generalmente requiere una malla detallada.
Para comprender la curvatura Gaussiana de un punto en una superficie, en primer lugar debe saber cuál es la curvatura de la curva.
En cualquier punto en una curva del plano, la línea que mejor se aproxima a la curva que atraviesa este punto es la línea tangente. También podemos encontrar el círculo más aproximado que atraviese este punto y sea tangente a la curva. La inversa del radio de este círculo es la curvatura de la curva en este punto.
El círculo más aproximado puede estar situado a la izquierda de la curva o a la derecha la curva. Si tenemos esto en cuenta, podemos establecer dar el símbolo positivo de curvatura si el círculo se encuentra a la izquierda y negativo si el círculo se encuentra a la derecha de la curva. Esto se denomina curvatura señalada.
La curvatura de sección normal es una generalización de la curvatura aplicada a las superficies. Dado un punto en la superficie y una dirección situada en el plano tangente de la superficie en ese punto, la curvatura de sección normal se calcula intersecando la superficie con el plano segmentado por el punto, la normal a la superficie en ese punto y la dirección. La curvatura de sección normal es la curvatura señalada de esta curva en el punto de interés.
Si miramos en todas las direcciones en el plano tangente a la superficie en nuestro punto y calculamos la curvatura de sección normal en todas esas direcciones, entonces habrá un valor máximo y un valor mínimo.
Curvatura gaussiana
La curvatura gaussiana de una superficie en un punto es el producto de las curvaturas principales en ese punto. El plano tangente de cualquier punto con curvatura gaussiana positiva toca la superficie en un sólo punto, mientras que el plano de cualquier punto con curvatura gaussiana negativa corta la superficie. Cualquier punto con un curvatura media de cero tiene una curvatura gaussiana negativa o de cero.
Curvaturas principales
Las curvaturas principales de una superficie en un punto son el mínimo y el máximo de las curvaturas normales en ese punto. (Las curvaturas normales son las curvaturas de las curvas en la superficie situadas en planos que incluyen el vector tangente en un punto determinado.) Las curvaturas principales se usan para calcular las curvaturas gaussianas y medias de la superficie.
Curvatura media
La curvatura Media de una superficie en un punto es el producto de las curvaturas principales en ese punto. Cualquier punto con un curvatura media de cero tiene una curvatura gaussiana negativa o de cero.
Las superficies con una curvatura media de cero en todas partes son superficies mínimas. Las superficies con una curvatura media constante en todas partes a menudo se conocen como superficies de curvatura media constante (CMC).
Las superficies CMC tienen la misma curvatura media en toda la superficie.
Los procesos físicos que pueden ser modelados por superficies CMC incluyen la formación de burbujas de jabón, tanto libres como asociadas a los objetos. Una burbuja de jabón, a diferencia de una simple capa de jabón, encierra un volumen y existe en un equilibrio donde la presión ligeramente mayor dentro de la burbuja queda compensada por las fuerzas de superficie mínima de la misma burbuja.
Las superficies mínimas son el subconjunto de superficies CMC donde la curvatura es cero en todas partes.
Los procesos físicos que pueden ser modelados por superficies mínimas incluyen la formación de capas de jabón que se extienden en objetos fijos, como bucles de estructura alámbrica. Una capa de jabón no se deforma por la presión del aire (que es igual en ambos lados) y es libre de minimizar su área. Por el contrario, una burbuja de jabón encierra una cantidad fija de aire y tiene presiones desiguales en el interior y el exterior.
|
DesactivarAnálisisDeCurvatura |
|
|
Cierre el cuadro de diálogo Curvatura. |
|
DesactivarAnálisisDeCurvatura
Desactiva la visualización del análisis de curvatura.
Menús
Acceso directo
Barras de herramientas