Curvatura
|
|
|
Círculo de curvatura |
|
Curvatura
Analiza la curvatura en un punto de una curva o superficie utilizando un radio de círculo.
Pasos
Seleccione una curva.
El radio de curvatura de la curva en el marcador se mostrará en la barra de estado y un círculo negro de ese radio se mostrará tangente a la curva en el marcador. También aparecerá una línea blanca tangente a la curva.
Los puntos blancos marcan los puntos de curvatura máxima en una parte de la curva donde la curvatura empieza a disminuir en ambas direcciones desde los puntos.
Los puntos negros marcan los puntos de curvatura mínima donde el círculo de curvatura salta de un lado de la curva al otro. La curvatura en los puntos negros siempre es de 0.
Designe para marcar la curvatura con un círculo o pulse Esc para finalizar el comando.
Para analizar la curvatura de una superficie
Seleccione una superficie.
A medida que mueve el cursor, aparecen dos medios círculos que muestran la curvatura mínima y máxima en ese punto de la curva.
Designe un punto en la superficie.
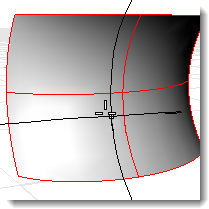
La siguiente información de evaluación de superficie aparecerá en el área de comandos:
Evaluación de la curvatura de superficie en la posición del parámetro
Punto 3D
Normal 3D
Curvatura principal máxima y mínima
Curvatura gaussiana
Curvatura media
Notas
Cada posición en una curva suave tiene un círculo que se aproxima mejor a la curva en esa posición.
El cursor queda restringido automáticamente a los puntos de inflexión de la curva (donde cambia el signo de la curvatura).
Cada posición en una superficie suave tiene dos círculos de este tipo. El círculo con un radio mayor siempre es ortogonal al círculo con un radio menor.
Las curvaturas principales son inversas a los radios de los arcos.
La curvatura gaussiana es positiva cuando ambos círculos señalan hacia la misma dirección, negativa cuando los círculos señalan direcciones opuestas y cero si uno de los círculos degenera en una línea.
Opciones
MarcarCurvatura
Se coloca un punto y el círculo de curvatura o la mitad de los círculos en el punto calculado de una curva.
De este modo, se tiene información permanente cuando el radio de curvatura es infinito (la curvatura es cero, la curva es localmente lisa, por ejemplo en puntos de inflexión donde la tangencia de la curva cambia de un lado al otro) y no se puede calcular. Esto no automatiza la localización de los puntos de inflexión, pero permite marcarlos manualmente.
Para comprender la curvatura Gaussiana de un punto en una superficie, en primer lugar debe saber cuál es la curvatura de la curva.
En cualquier punto en una curva del plano, la línea que mejor se aproxima a la curva que atraviesa este punto es la línea tangente. También podemos encontrar el círculo más aproximado que atraviese este punto y sea tangente a la curva. La inversa del radio de este círculo es la curvatura de la curva en este punto.
El círculo más aproximado puede estar situado a la izquierda de la curva o a la derecha la curva. Si tenemos esto en cuenta, podemos establecer dar el símbolo positivo de curvatura si el círculo se encuentra a la izquierda y negativo si el círculo se encuentra a la derecha de la curva. Esto se denomina curvatura señalada.
La curvatura de sección normal es una generalización de la curvatura aplicada a las superficies. Dado un punto en la superficie y una dirección situada en el plano tangente de la superficie en ese punto, la curvatura de sección normal se calcula intersecando la superficie con el plano segmentado por el punto, la normal a la superficie en ese punto y la dirección. La curvatura de sección normal es la curvatura señalada de esta curva en el punto de interés.
Si miramos en todas las direcciones en el plano tangente a la superficie en nuestro punto y calculamos la curvatura de sección normal en todas esas direcciones, entonces habrá un valor máximo y un valor mínimo.
Curvatura gaussiana
La curvatura gaussiana de una superficie en un punto es el producto de las curvaturas principales en ese punto. El plano tangente de cualquier punto con curvatura gaussiana positiva toca la superficie en un sólo punto, mientras que el plano de cualquier punto con curvatura gaussiana negativa corta la superficie. Cualquier punto con un curvatura media de cero tiene una curvatura gaussiana negativa o de cero.
Curvaturas principales
Las curvaturas principales de una superficie en un punto son el mínimo y el máximo de las curvaturas normales en ese punto. (Las curvaturas normales son las curvaturas de las curvas en la superficie situadas en planos que incluyen el vector tangente en un punto determinado.) Las curvaturas principales se usan para calcular las curvaturas gaussianas y medias de la superficie.
Curvatura media
La curvatura Media de una superficie en un punto es el producto de las curvaturas principales en ese punto. Cualquier punto con un curvatura media de cero tiene una curvatura gaussiana negativa o de cero.
Las superficies con una curvatura media de cero en todas partes son superficies mínimas. Las superficies con una curvatura media constante en todas partes a menudo se conocen como superficies de curvatura media constante (CMC).
Las superficies CMC tienen la misma curvatura media en toda la superficie.
Los procesos físicos que pueden ser modelados por superficies CMC incluyen la formación de burbujas de jabón, tanto libres como asociadas a los objetos. Una burbuja de jabón, a diferencia de una simple capa de jabón, encierra un volumen y existe en un equilibrio donde la presión ligeramente mayor dentro de la burbuja queda compensada por las fuerzas de superficie mínima de la misma burbuja.
Las superficies mínimas son el subconjunto de superficies CMC donde la curvatura es cero en todas partes.
Los procesos físicos que pueden ser modelados por superficies mínimas incluyen la formación de capas de jabón que se extienden en objetos fijos, como bucles de estructura alámbrica. Una capa de jabón no se deforma por la presión del aire (que es igual en ambos lados) y es libre de minimizar su área. Por el contrario, una burbuja de jabón encierra una cantidad fija de aire y tiene presiones desiguales en el interior y el exterior.
Barras de herramientas
Menús
Acceso directo